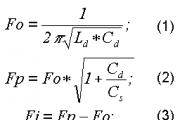Электростатическая теорема гаусса и ее физический смысл. Образовательный портал тгу

Вычисление напряженности поля системы неподвижных электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, применяя выведенную немецким ученым К. Гауссом (1777 - 1855) теорему, определяющую поток вектора напряженности сквозь произвольную замкнутую поверхность.

Воспользуемся графической картиной описания электростатического поля (с помощью силовых линий), пусть густота силовых линий равна модулю Е - E, а поле однородно. Тогда вектор напряженности поля в каждой его точке имеет лишь одно направление и постоянен по величине, а линии напряженности параллельны вектору напряженности. Введем понятие потока вектора напряженности. Будем обозначать эту величину так: Ф Е.

Потоком вектора Е называют число силовых линий, пронизывающих элементарную площадку dS, нормаль n которой составляет угол a с вектором Е (E n = E cosa).

где интеграл берется по замкнутой поверхности S .

Принято для замкнутых поверхностей нормаль брать наружу области, т.е. выбирать внешнюю нормаль.

Поток вектора величина алгебраическая , она зависит не только от конфигурации поля Е , но и от выбора направления нормали. Понятие потока относится к любому векторному полю . Вычисление напряжённости поля системы электрических зарядов существенно упрощается с применением электростатической теоремы Гаусса , которую мы в дальнейшем в разделе «Электростатика» для краткости будем называть просто теоремой Гаусса.

Теорема Гаусса определяет поток вектора напряжённости электростатического поля через произвольную замкнутую поверхность.

В СИ [Ф E ] = 1 В´м.

Сначала рассчитаем поток вектора напряженности сквозь сферическую поверхность радиуса r , охватывающую точечный заряд q , находящийся в её центре, он равен:

.

Эта формула справедлива для замкнутой поверхности любой формы, если окружить сферу произвольной замкнутой поверхностью, то каждая линия напряжённости, пронизывающая сферу пройдёт и сквозь эту поверхность.

Рис. 10.2. Расчет потока вектора напряженности для сферической поверхности радиуса r

Пусть произвольная замкнутая поверхность охватывает заряд q. Поток считается положительным, если линии напряженности выходят из поверхности, и, отрицательным, если линии напряженности входят в поверхность . Нечетное число пересечений при вычислении потока сводится к одному пересечению. Сформулирует теорему Гаусса для электростатического поля.

Поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную e 0 .

.

Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским (1801 - 1862), а затем независимо от него применительно к электростатическому полю - К. Гауссом.

Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен 0 .

Пусть произвольная поверхность окружает N зарядов, тогда Е = SЕ i и поток вектора напряженности:

.

В то время как само поле Е зависит от конфигурации всех зарядов , то поток вектора Е сквозь произвольную замкнутую поверхность S определяется только алгебраической сум- мой зарядов внутри поверхности S. Если передвинуть заряды без пересечения поверхности S , то поток вектора Е через эту поверхность останется прежним.

Скалярное произведение векторов E и dS называетсяпотоком вектора напряженности dФ Е через площадку dS (рис. 1.2.): dФ E = Е∙ dS = Е∙ dS cosa= Е n dS , где a – угол между векторами n и Е ; Е n = Е cosa – проекция вектора Е на нормаль n к площадке dS .

Если плоская поверхность S перпендикулярна силовым линиям однородного электрического поля, то поток напряженности через нее

Ф Е = Е∙S .

Для неоднородных полей поток напряженности поля через всю поверхность представится суммой элементарных потоков:

.

Единицей измерения потока вектора напряженности электростатического поля является вольт-метр (В·м). Поток вектора напряженности электростатического поля зарядов q в вакууме (e = 1) через сферическую поверхности радиусом R , охватывающую этот заряд, находящийся в ее центре (рис.25):

Во всех точках сферы |E| одинакова, и силовые линии перпендикулярны поверхности. Следовательно, . Площадь поверхности сферы равна 4pR 2 . Отсюда

.

На рис. 26 представлена произвольная замкнутая поверхность, охватывающая заряд q >0. Некоторые линии напряженности то выходят из поверхности, то входят в нее. Нечетное число пересечений сводится к одному: линии, выходящие из поверхности – положительные, а линии, входящие – отрицательные. Если замкнутая поверхность не охватывает заряд, то Ф Е = 0. Если замкнутая поверхность охватывает несколько зарядов, то

Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную e 0 .

Эта формулировка представляет собой теорему К. Гаусса.

Применяя теорему Гаусса, можно определить напряженности полей, создаваемых заряженными телами различной формы:

где величина называется поверхностной плотностью заряда .

Работа сил электростатического поля при перемещении заряда. Циркуляция вектора напряженности электростатического поля. Потенциальная энергия и потенциал электростатического поля

При перемещении заряда в электростатическом поле действующие на заряд кулоновские силы совершают работу. Пусть точечный заряд q 0 > 0 перемещается в поле другого точечного заряда q > 0 из точки С в точку В вдоль произвольной траектории (рис.27). При элементарном перемещении заряда на dl эта сила совершает работу dA :

dA = F ·dl = F dl cosa,

где a – угол между векторами F и dl ; dl cosa = dr – проекция вектора dl на направление силы F . Таким образом,

dA = F dr , .

Полная работа по перемещению заряда q 0 из точки С в точку В определяется интегралом

где r 1 и r 2 – расстояния от заряда q до точек С и В. Из полученной формулы следует, что работа, совершаемая при перемещении заряда q 0 в поле заряда q , не зависит от формы траектории движения, а зависит только от начального и конечного положений заряда . Следовательно, электростатическое поле точечного заряда – потенциальное , а действующие в нем силы – консервативные .

Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L , равна нулю, т.е. Так как dA = F dl и F = E q 0 , то dA = q 0 E dl . Отсюда получаем . Если заряд q 0 является единичным положительным точечным, то получим

,

где E l = E cosa – проекция вектора Е на направление элементарного перемещения dl . Интеграл называется циркуляцией вектора напряженности . Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю . Это заключение справедливо для потенциального поля.

Работа в таком поле совершается за счет убыли потенциальной энергии:

A = – ΔW п = W п1 – W п2 .

Используя формулу работы силы электростатического поля по перемещению заря­да, получим

= = W п1 – W п2 .

Анализируя полученное выражение, можно сделать вывод, что потенциальная энергия точечного заряда q 0 в поле заряда q равна

.

Если поле создано системой зарядов q 1 , q 2 , ..., q n , то потенциальная энергия заряда q 0:

.

Потенциальная энергия заряда q 0 зависит от его величины. Однако отношение потенциальной энергии заряда q 0 к его величине является постоянным для данной точки поля и может служить энергетической характеристикой данной точки поля. Отношение называется потенциалом электростатического поля j:

.

Потенциал j– скалярная физическая величина, численно равная потенциальной энергии единичного положительного заряда, помещенного в данную точку поля.

Ранее было записано A = W п1 – W п2 . Так как W п1 = φ 1 q 0 и
W п2 = φ 2 q 0 , то A = q 0 (φ 1 – φ 2) и Δ φ = (φ 1 – φ 2) = .

Разность потенциалов Δφ двух точек поля численно равна работе сил поля по перемещению единичного положительного заряда из точки 1 в точку 2.

Если заряд q 0 перемещать из какой-либо точки поля в бесконечность, то r 2 ® ¥, W п2 = 0 и φ 2 = 0. Тогда работа A ∞ по перемещению заряда q 0 в бесконечность:

A ∞ = q 0 φ 1 , φ 1 = .

Потенциал точки поля численно равен работе, совершае­мой электрическими силами при перемещении единичного положительного заряда из данной точки поля в бесконечность .

Потенциал точки поля системы зарядов q 1 , q 2 ,..., q n равен алгебраической сумме потенциалов полей всех этих зарядов:

.

Единицей потенциала является вольт (В).

Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, потенциал всех точек которых одинаков. Если поле создано точечным зарядом, эквипотенциальные поверхности в данном случае – концентрические сферы, а линии напряженности перпендикулярны эквипотенциальным поверхностям (рис.27).

Рассмотрим площадку А , которую пронизывают силовые линии однородного электрического поля напряженностью Е (рис. 23.1).

Площадка может иметь форму прямоугольника (как на рисунке), круга или любую другую. Если напряженность электрического поля перпендикулярна площадке (рис. 23.1, а), то поток напряженности Ф E через нее определяется как

Ф E = ЕА

Если площадка А не перпендикулярна Е , а составляет с Е некоторый угол θ (рис. 23.1,6), то ее будет пронизывать меньше силовых линий. В этом случае поток напряженности через площадку будет определяться формулой:

Ф E = ЕА ⊥ = EAcosθ (поле Е однородно), (23.1а)

Здесь А ⊥ - проекция площадки А на плоскость, перпендикулярную Е .

Площадку А ⊥ можно представить вектором, направленным перпендикулярно ее поверхности, а по величине пропорциональным площади (рис. 23.1,6). Тогда θ - угол между Е и А , и поток напряженности можно записать в виде произведения двух векторов: Ф E = ЕА [поле Е однородно]

В силу принятого нами определения поток напряженности допускает наглядное толкование, основанное на понятии силовых линий. Число силовых линий N , проходящих через единичную площадку, перпендикулярную направлению поля (А ⊥ ), пропорционально напряженности электрического поля: Е ~ N/A ⊥ . Следовательно:

N ~ ЕА ⊥ = Ф E

т.е. поток напряженности поля через площадку пропорционален числу силовых линий, пересекающих ее поверхность.

Рассмотрим теперь более общий случай, когда электрическое поле Е неоднородно, а поверхность не плоская (рис. 23.2). Разобьем эту поверхность на п элементов, площади которых обозначим ΔА 1 , ΔА 2 , ... , ΔА n . Разбиение должно быть таким, чтобы можно было считать каждый элемент ΔA i плоским и электрическое поле в пределах элемента однородным. Тогда поток напряженности через всю поверхность будет суммой

где E i - напряженность поля, отвечающая элементу ΔA i . В пределе ΔA i > 0 сумма переходит в интеграл по всей поверхности, и равенство становится точным:

Ф E = ∫Е · dА

Во многих случаях (и, в частности, в случае теоремы Гаусса) мы имеем дело с потоком через замкнутую поверхность, т.е. через поверхность, ограничивающую замкнутый объем, подобно шару или футбольному мячу (рис. 23.3)

До сих пор мы не учитывали существование неоднозначности в выборе направления вектора A ; например, на рис. 23.1 вектор А может быть направлен как вправо вверх, так и влево вниз-в любом случае он все равно будет перпендикулярен поверхности. В случае замкнутой поверхности условились направлять вектор А (или dA ) наружу из ограниченного поверхностью объема (рис. 23.4).

Для силовой линии, выходящей из объема (справа на рис. 23.4), угол θ между Е и dA меньше π/2 и cosθ > 0; для линии, входящей в объем (слева на рис. 23.4), 0 > π/2 и cosθ поток, входящий в замкнутый объем, отрицателен (∫Е · cosθdА . Формула (23.3) дает, таким образом, величину потока, выходящего из объема, ограниченного замкнутой поверхностью. Если значение Ф E отрицательно, то результирующий поток направлен внутрь объема.

На рис. 23.3 число линий, входящих в объем, равно числу выходящих линий. Поэтому Ф E = 0: результирующий поток через поверхность равен нулю. Поток ∫Е · dА oтличен от нуля лишь в том случае, когда какое-то число силовых линий начинается или заканчивается внутри замкнутой поверхности. А поскольку силовые линии могут начинаться или заканчиваться только на электрических зарядах, поток будет отличен от нуля лишь в том случае, когда суммарный заряд внутри поверхности не равен нулю. Например, поверхность А 1 на рис. 23.5 окружает положительный заряд, и поток напряженности электрического поля через эту поверхность направлен наружу (Ф E > 0); внутри поверхности А 2 заключен такой же по величине отрицательный заряд, и поток направлен внутрь этой поверхности (Ф E Ф E зависит от заряда, и именно в этом состоит суть теоремы Гаусса.

Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью пронизывают некоторую площадкуS , топоток вектора напряженности (число силовых линий через площадку) будет определяться формулой

где E n – произведение векторана нормальк данной площадке (рисунок 2.5).

Рисунок 2.5

Полное число силовых линий, проходящих через поверхность S , называется потоком вектора напряженности Ф Е через эту поверхность.

Элементарный поток вектора напряженности через площадку dS (рис. 5) определится соотношением:

где

– проекция

на направление нормали.

В векторной форме можно записать

– скалярное произведение двух векторов, где вектор

.

Таким образом, поток вектора есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным .

Полный поток вектора напряженности через любую площадку S можно определить тогда

, а поток через замкнутую поверхность, окружающую заряд или заряженное тело равен

.

Так как напряженность поля, созданного в любой точке пространства зависит от величины заряда, создающего это поле, то поток вектора напряженности электростатического поля через любую площадку, находящуюся в этом поле также зависит от величины заряда.

Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.

Рисунок 2.6 Рисунок 2.7

Для рисунка 2.6 – поверхность А 1 окружает положительный заряд и поток здесь направлен наружу, т.е.

ПоверхностьА 2 – окружает отрицательный заряд, здесь

и направлен внутрь. Общий поток через поверхностьА равен нулю.

Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность А отрицательный.

Таким образом, поток вектора напряженности зависит от заряда.

2.3. Теорема Остроградского – Гаусса (теорема Гаусса)

К.Ф. Гаусс (1777–1855) выдающийся немецкий математик, астроном и физик в 1839г. предложил теорему, которая устанавливает связь потока вектора напряженности электрического поля череззамкнутую поверхность со значением зарядаq , находящегося внутри этой поверхности.Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.

Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :

.

Докажем эту теорему. Пусть поле создается точечным зарядом q . Окружим заряд замкнутой поверхностьюS произвольной формы. Разобьем замкнутую поверхность на элементарные площадкиdS , к каждой из которых проведем вектор нормали.

Элементарный поток вектора напряженности через площадкуdS (рис. 2.8) определится соотношением:

где

–проекция

на направление нормали. Тогда

, где

- элементарный телесный угол, под которым элемент

виден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхностьS от точечного зарядаq , находящегося внутри этой поверхности.

,

так как

, то

.

Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS 1 иdS 2 , находящиеся внутри телесного углаd Ω(рис. 2.9) равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Тогда , следовательно, поток напряженности электрического поля через любую поверхностьS , не охватывающую заряды равен нулю, т.е.Ф Е =0.

Пусть внутри замкнутой поверхности имеется зарядов, тогда алгебраическим суммированием (согласно принципу суперпозиции) находим, что общий поток вектора напряженности через замкнутую поверхность равен

.

Теорема доказана.

Таким образом теорему Гаусса можно сформулировать следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :

(1),

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то теорема Гаусса имеет вид:

(2)

где интеграл справа берется по объему V, охватываемому поверхностьюS .

Необходимо обратить внимание на следующее обстоятельство: в то время как само поле зависит от конфигурации всех зарядов, поток

сквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхностиS . Это значит, чтоесли передвинуть заряды внутри замкнутой поверхности , тоизменится всюду , и на поверхностиS , апоток вектора через эту поверхность останется прежним .

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по т еореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на , то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.

Рассмотрим примеры применения теоремы Гаусса.

Исследование электростатических полей с помощью электролической ванны

Теоретическое введение

Основные характеристики электростатического поля.

Электростатическое поле - это поле посредством которого взаимодействуют неподвижные электричекие заряды. Для обнаружения и исследования поля вводят понятие пробный заряд. Пробный заряд - это положительный, точечный заряд, не искажающий исследуемое поле (точечный заряд - это заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстояниями до других запрядов). На пробный заряд Q 0 , внесенный в электрическое поле, создаваемое точечным зарядом Q , действует кулоновская сила:

где - вектор, проведенный от заряда Q к заряду Q 0 . Отношение не зависит от величины внесенного заряда Q 0 , т.е. является характеристикой самого поля.

Напряженность электростатического поля является векторной силовой характеристикой поля и численно равна силе, с которой поле действует на единичный пробный заряд, внесенный в данную точку поля:

Единицей напряженности является 1 Н/Кл - это напряженность такого электростатического поля, которое на заряд в 1 Кл действует с силой в 1 Н. Напряженность также выражают в В/м.

Для графического изображения электростатического поля используют линии напряженности вектора (силовые линии). Эти линии проводятся таким образом, чтобы касательные к ним в каждой точке поля совпадали с направлением вектора напряженности в этой точке. Силовые линии не пересекаются и направлены от положительного заряда к отрицательному. По густоте силовых линий можно судить о величине напряженности. Условились считать, что напряженность в данной точке пространства равна числу линий напряженности, пересекующих единичную площадку, поставленную перпендикулярно линиям напряженности. Поле однородно, если во всех точках пространства оно одинаково.

Если поле создается системой зарядов, то результирующая сила, действующая на пробный заряд, внесенный в данную точку поля, равна геометрической сумме сил, действующих на пробный заряд со стороны каждого точечного заряда в отдельности. Поэтому напряженность в данной точке поля равна:

Это соотношение выражает принцип суперпозиции полей : напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым зарядом в отдельности.

Введем понятие потока вектора напряженности электрического поля. Расположим в электрическом поле элементарную площадку dS , в пределах которой поле можно считать однородным. Ориентация этой площадки в пространстве задается единичным вектором нормали . Единичный вектор нормали можно построить в двух противоположных направлениях. Одно из них условно принимается за положительное, в этом направлении и проводится нормаль . В случае замкнутой поверхностя принято нормаль брать наружу области, охватываемой этой поверхностью. Тогда вектор – численно равен dS , а его направление совпадает с направлением нормали .

Потоком вектора напряженности электрического поля через поверхность dS называется скалярное произведение векторов и :

где - угол между векторами и , –проекция вектора на направление нормали .

Поток вектора через произвольную поверхность S :

Поток вектора является алгебраической величиной: если угол - острый, то и ; если угол - тупой, то и .

Теорема Гаусса для напряженности электростатического поля :

Поток вектора напряженности электрического поля через произвольную замкнутую поверность равен алгебраической сумме всех зарадов, расположенных внутри этой поверхности, деленной на :

Если в электрическое поле E 0 , создаваемое свободными зарядами , поместить диэлектрик, то он поляризуется и на поверхности появляется нескомпенсированный заряд с поверхностной плотностью . Нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Этим термином подчеркивается, что свобода перемещения связанных зарядов ограничена. Они могут смещаться лишь внутри электрически нейтральных молекул. При однородной поляризации в объеме диэлектрика происходит компенсация положительных и отрицательных зарядов молекул, и никаких макроскопических связанных зарядов не появляется.

Связанные заряды, возникающие на поверхности диэлектрика, создают электростатическое поле внутри диэлектрика. Это поле направлено в противоположную сторону внешнему полю E 0 . Результирующее поле внутри диэлектрика: E = E 0 - E " , где E " - поле, создаваемое связанными зарядами:

Таким образом, результирующее поле внутри диэлектрика:

Найдем связь между поверхностной плотностью связанных зарядов и поляризованностью. Для этого кусок однородного диэлектрика, имеющий форму косого цилиндра, поместим в однородное электрическое поле, направленное параллельно оси цилиндра. На основаниях цилиндра появятся связанные заряды с поверхностной плотностью . На боковых гранях связанных зарядов не возникнет, т.к. смещение зарядов внутри диэлектрика происходит параллельно этим граням. Если S – площадь основания цилиндра, то диэлектрик приобретет дипольный момент:

где V – объем цилиндра. Пусть - единичный вектор внешней нормали к основанию цилиндра, заряженному положительно. Тогда

Эта формула выведена для положительнозаряженного основания, но она верна и для отрицательнозаряженного основания, т.к. в этом случае внешняя нормаль направлена в противоположную сторону, а, следовательно, проекция отрицательна. Формула верна и для боковой поверхности цилиндра, т.к. на ней . Формула показывает, что нормальная составляющая поляризованностипредставляет собой по величине заряд, смещенный при поляризации через единичную площадку в направлении нормали к ней. Если диэлектрик выбрать в форме прямоугольного параллелепипеда, то

где - диэлектрическая восприимчивость вещества.

Подставим (9) в (8), а затем получивщееся выражение в (3):

Таким образом, - диэлектрическая проницаемость среды, показывает во сколько раз поле внутри диэлектрика меньше поля в вакууме. Как видно из формулы, напряженность электростатического поля зависит от свойств среды.

При неоднородной поляризации связанные заряды могут появиться не только на поверхности, но и в объеме диэлектрика. Вычислим заряд, появляющийся внутри диэлектрика при неоднородной поляризации. Выделим мысленно в диэлектрике произвольный объем V , ограниченный замкнутой поверхностью S . Заряд, смещенный при поляризации через площадку dS в отрицательном направлении нормали равен . Через всю поверхность S внутрь объема V при поляризации поступает поляризационный заряд:

Подставим в данное выражение

.

Следовательно,

.

Введем новый вектор

Это и есть теорема Гаусса для электростатического поля в диэлектрике. Из формулы (13) видно, что поток вектора D через замкнутую поверхность определяется только свободными зарядами. Формулировка теоремы Гаусса для поля D : поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, охватываемых этой поверхностью.

Подставив в (12) выражение (9) получим:

Таким образом вектора D и E связаны соотношением:

Глубокого физического смысла D не имеет. Вектор Е задает поле в диэлектрике и зависит от свойств среды. На поле Е 0 , которое создается свободными зарядами, накладывается поле связанных зарядов. Вектор D от свойств среды не зависит, поэтому характеризует поле свободных зарядов, но такое, которое имеет место в присутствии связанных зарядов.

Заряды, расположенные во внешнем (по отношению к этой поверхности) пространстве на величину потока не влияют.

Поместим в электростатическое поле точечного заряда Q заряд Q 0 . Пусть заряд Q 0 перемещается вдоль произвольной траектории из точки 1 в точку 2.

При этом сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна:

,

.

Работа при перемещении заряда Q 0 из точки 1 в точку 2:

Интеграл - называется циркуляцией вектора напряженности. Т.о. теорема о циркуляции : циркуляция вектора напряженности электростатического поля равна нулю. Из теоремы о циркуляции следует, что силовые линии не могут быть замкнутыми: они начинаются и кончаются на зарядах или уходят в бесконечность. Физический смысл теоремы о циркуляции заключается в том, что электрическое поле - потенциально.

Заряд Q 0 , находящийся в электростатическом поле, обладает потенциальной энергией W . Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу сил элктростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q 0 в начальной и конечной точках:

Отношение W/Q 0 не зависит от величины Q 0 и является поэтому энергетической характеристикой электростатического поля, называемой потенциалом:

а элементарная работа

Элементарную работу dA , совершаемую силами электростатического поля, можно, по определению, представить в виде скалярного произведения и его потенциалом

Векторная величина, называемая градиентом потенциала, указывает направление наиболее быстрого возрастания потенциала. Знак минус показывает, что вектор напряженности поля направлен в сторону убывания потенциала.

Для графического представления потенциала используют эквипотенциальные поверхности - это поверхности, во всех точках которых потенциал имеет одно и тоже значение. Покажем, что эквипотенциальные поверхности перпендикулярны линиям напряженности электростатического поля. Будем перемещать заряд Q 0 вдоль эквипотенциальной поверхности:

Т.к. заряд перемещается вдоль эквипотенциальной поверхности, то

но . Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальную поверхность можно провести через любую точку поля, следовательно, таких поверхностей можно провести бесконечно много. Условились проводить эквипотенциальные поверхности так, чтобы разность потенциалов между соседними поверхностями была всюду одинакова. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля. Чем гуще расположены поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности, следовательно, тем больше в данном месте , а значит и .

При конструировании электронных ламп, конденсаторов, электронных линз и других приборов часто требуется знать распределение электрического поля в пространстве между электродами сложной формы. Аналитический расчет поля удается только при самых простых конфигурациях электродов и в общем случае невыполним. Для исследования сложных электростатических полей используется метод электролитической ванны (метод зондов), в котором экспериментально определяется положение линий равного потенциала, что позволяет построить силовые линии поля и найти напряженность в различных его точках.

Электролитическая ванна, изготовленная из хорошего диэлектрика (оргстекло), заполнена тонким слоем жидкого электролита (водой), проводимость которого мала по сравнению с проводимостью металла. В ванну помещают металлические электроды А и В , поле между которыми хотят изучить. Электроды опираются на дно ванны и возвышаются над поверхностью воды. В данной работе исследуются электростатические поля, создаваемые плоскопараллельными пластинами конечных размеров, пластиной и точечным зарядом, двумя коаксиальными цилиндрами.

На электроды от источника питания подается напряжение U o , которое контролируется вольтметром.

Потенциал в различных точках поля измеряется с помощью зонда, который подсоединен к цифровому вольтметру.

На дне электролитической ванны расположена координатная сетка. При выполнении работы с помощью этой сетки на отдельном листе бумаги (миллиметровке) показывается положение электродов и строится картина электрического поля – эквипотенциальные линии. По данным эксперимента вычисляют величину напряженности в различных точках электрического поля.