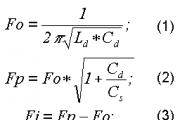Напряженность поля равномерно заряженной тонкой нити. Применение теоремы Гаусса для расчёта электрических полей

Рассмотрим поле, созданное зарядом, равномерно распределенным по бесконечной нити. Эту задачу мы решили на прошлой лекции, воспользовавшись принципом суперпозиции электрических полей (см. 1.11).

Теперь покажем, несколько проще можно рассчитать это поле с помощью теоремы Гаусса.

Определим напряжённость поля на расстоянии r от нити, заряженной с постоянной линейной плотностью:

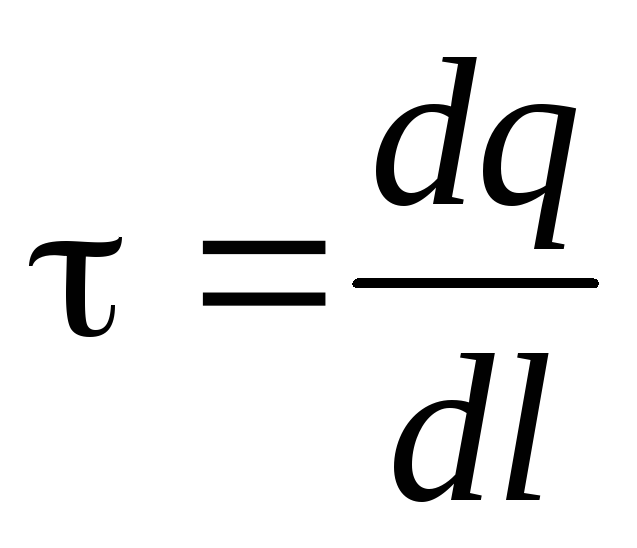, [Кл/м] (2.10)

Окружим нить замкнутой цилиндрической поверхностью (рис. 2.7.). Высота цилиндра - h , а радиус его основания -r .

Рис. 2.7.

Поле, созданное заряженной нитью, обладает цилиндрической симметрией. В связи с этим векторы напряжённости во всех точках боковой поверхности цилиндра будут одинаковы по модулю и направлены радиально, то есть перпендикулярно к боковой поверхности цилиндра. На основаниях цилиндра векторы , направленные по-прежнему радиально, «скользят» по основанию, образуя прямой угол с нормалью.

Вычислим поток вектора через поверхность выбранного цилиндра. Полный поток через эту замкнутую «гауссову» поверхность складывается из потока через боковую поверхность цилиндра и через два его основания:

Последние два интеграла равны нулю, так как «скользящие» по основаниям цилиндра векторы не пронизывают их и не создают никакого потока. Формально эти два интеграла равны нулю, так как между векторамиипрямой угол и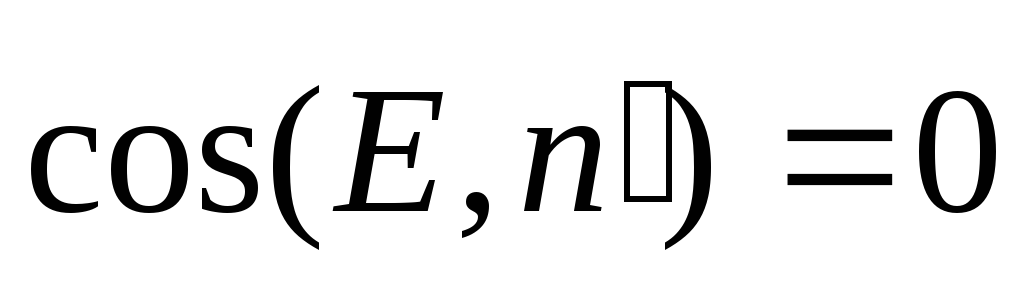

. Таким образом

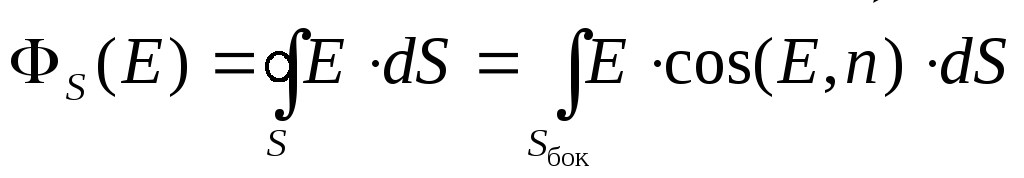
Во всех точках боковой поверхности цилиндра E =Е r =constи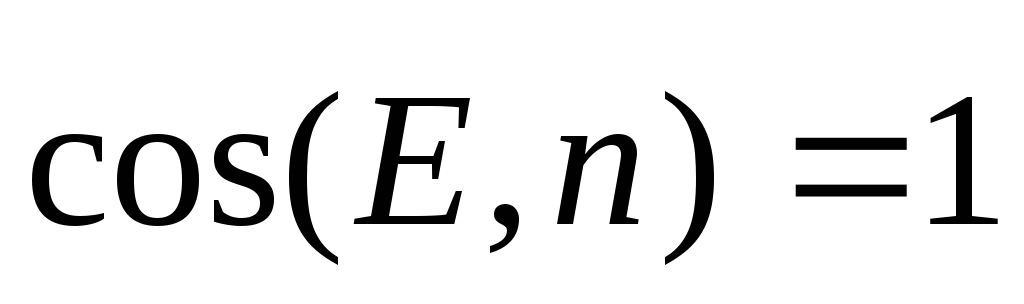

.

Поэтому поток через боковую поверхность цилиндра равен

(2.11)

Это поток вектора напряжённости электрического поля, вычисленный по определению потока.

Теперь воспользуемся теоремой Гаусса, отметив предварительно, что «заряд, заключённый внутри гауссовой поверхности» в данном случае сосредоточен на отрезке нити h - на оси цилиндра:

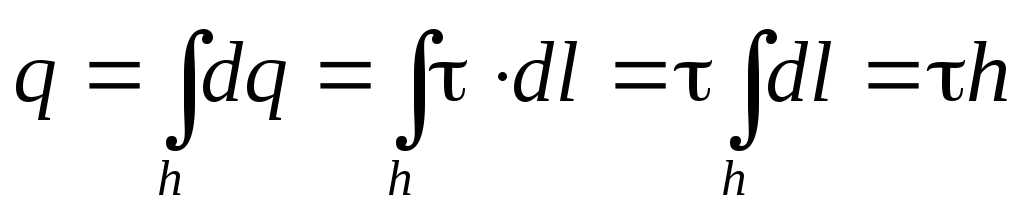
Таким образом

(2.12)

Отсюда теперь легко получить знакомую нам гиперболическую зависимость напряжённости поля от расстояния до нити - r (см. 1.11).

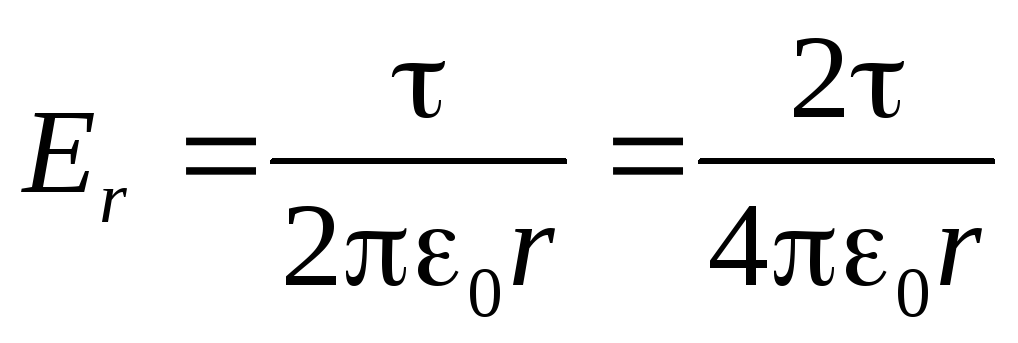(2.13)

1. Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора

Пусть электрическое поле создаётся зарядом, равномерно распределённым по поверхности безграничной плоскости, с поверхностной плотностью (рис. 2.8.)

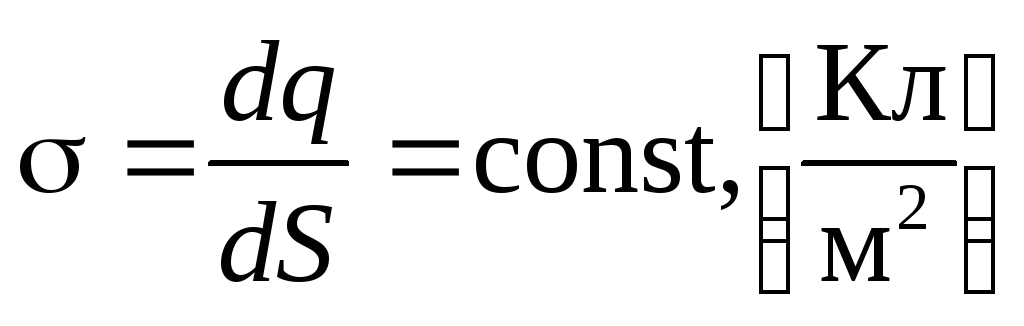
Рис. 2.8.

Из симметрии задачи следует, что поле повсюду направлено перпендикулярно к поверхности. Выясним, как меняется напряжённость поля по мере удаления от заряженной плоскости.

В качестве гауссовой поверхности удобно выбрать цилиндр. Ось цилиндра направим перпендикулярно плоскости, его основание расположим на расстоянии Х симметрично по обе стороны от поверхности.

Вычислим поток вектора напряжённости через боковую поверхность и основания цилиндра. Как следует из рис. 2.8., поток вектора напряжённости через боковую поверхность цилиндра равен нулю, так как здесь повсюду векторы напряжённости «скользят» по поверхности и

.

Тогда полный поток через замкнутую цилиндрическую поверхность можно записать как поток через два основания цилиндра.

Это величина, рассчитанная по определению потока.

Теперь воспользуемся теоремой Гаусса, заметив, что заряд q , «находящийся внутри гауссовой поверхности», в данном случае сосредоточен на площадкеS =S осн, «вырезанной» цилиндром на бесконечной плоскости

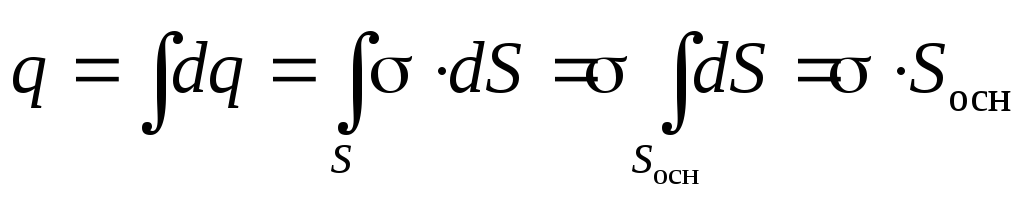(2.15)

Объединим результаты(2.15) и (2.14) в уравнение Гаусса:

Откуда следует

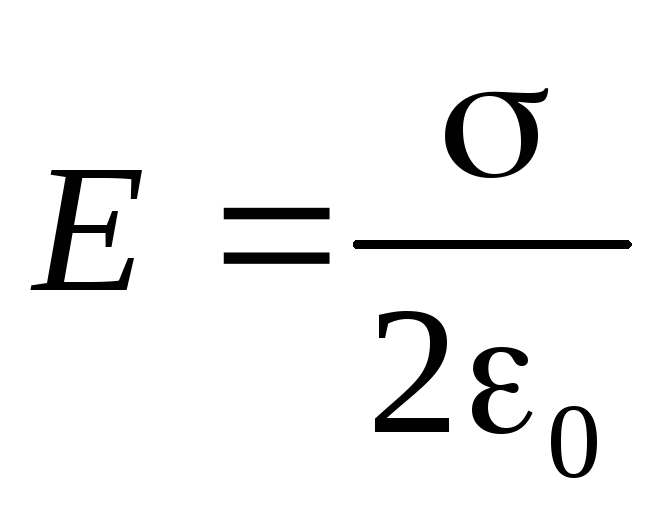(2.16)

Вывод. Поле, созданное бесконечной равномерно заряженной плоскостью, однородно. Оно не меняется с расстоянием от заряженной поверхности ни по величине, ни по направлению.

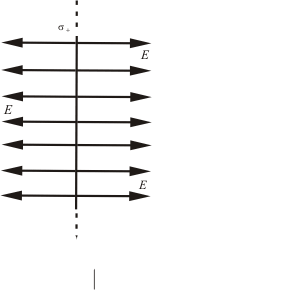
Теперь рассмотрим еще один важный пример. Пусть поле создаётся двумя бесконечными плоскостями, заряженными разноименно, но с одинаковой по величине поверхностной плотностью заряда (рис. 2.9.). Это важная идеализация электростатики - плоский конденсатор . Каждая обкладка этого конденсатора создаёт однородное поле, напряжённость которого мы только что установили (2.16):

.

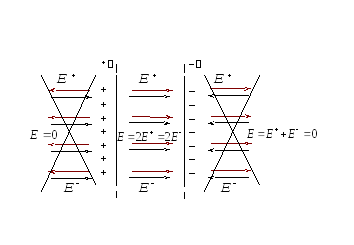
Рис. 2.9.

Силовые линии поля положительно заряженной плоскости направлены от неё, а отрицательной - к плоскости. При сложении этих полей, напряжённость результирующего поля вне конденсатора оказывается равной нулю, а внутри конденсатора, где эти поля совпадают по направлению, - поле удваивается:

. (2.17)

Пусть поле создается точечным электрическим зарядом q. Проведем замкнутую сферическую поверхность площадью S (рис. 1), окружающую этот заряд, центр которой совпадает с точкой нахождения заряда. Вычислим поток вектора напряженности через эту поверхность. За положительное направление нормали выберем направление внешней нормали . В этом случае во всех точках сферической поверхности E = const и cos = 1.

Модуль напряженности поля на расстоянии R от заряда

Площадь поверхности сферы

Следовательно, поток вектора напряженности через сферическую поверхность

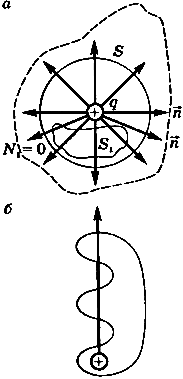
Полученный результат будет справедлив и для поверхности произвольной формы, а также при любом расположении заряда внутри этой поверхности. Действительно, если окружить сферу произвольной замкнутой поверхностью (рис. 2, а - поверхность изображена штрихами), то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 2, б), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в поверхность, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линии, входящей в поверхность. Если же внутри поверхности площадью S 1 (см. рис. 2) заряды отсутствуют, то поток напряженности через эту поверхность равен нулю (N S = 0).

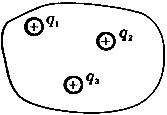
Если рассматриваемая поверхность охватывает не один, а несколько электрических зарядов, то под q следует понимать алгебраическую сумму этих зарядов (рис. 2) и

Эта формула выражает теорему Остроградского-Гаусса : поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на произведение электрической постоянной и диэлектрической проницаемости среды.

Применим эту теорему для расчета электростатических полей некоторых проводников.

Равномерно заряженная бесконечная плоскость

Пусть - поверхностная плотность заряда на плоскости (рис. 3).

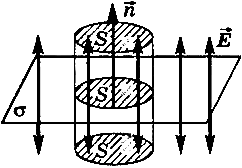
В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности ( = 90°, cos = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q = S, поэтому, согласно теореме Остроградского-Гаусса,

где = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости

Бесконечная равномерно заряженная нить

Пусть - линейная плотность заряда нити. Выделим участок нити длиной и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 4).

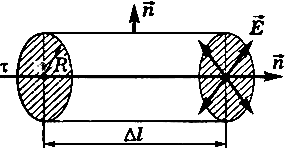
Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность , где R - радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю ( = 90°, cos = 0). Тогда полный поток напряженности через выделенный цилиндр

Заряд, находящийся внутри этого цилиндра, .

Согласно теореме Остроградского-Гаусса, можно записать

Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее,

Использование теоремы Гаусса для расчета полей эффективно в тех случаях, когда поле обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической). Симметрия и конфигурация поля должны быть такими, чтобы, во-первых, заряженное тело можно было бы окружить достаточно простой замкнутой поверхностью и, во-вторых, вычисление потока вектора напряженности свести к простому умножению Е (или E n) на площадь поверхностиSили часть ее. Если этого сделать нельзя, то задачу необходимо решать другими методами.

1. Поле равномерно заряженной бесконечной плоскости

Будем считать заряд положительным. Плоскость заряжена с постоянной поверхностной плотностью . Из симметрии вытекает, что напряженность в любой точке поля имеет направление, перпендикулярное к плоскости (рис. 2.10). Очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению.

Выделим на заряженной плоскости площадку

. Окружим эту площадку замкнутой поверхностью. В качестве замкнутой поверхности представим цилиндрическую поверхность с образующими, перпендикулярными к плоскости и основаниями величины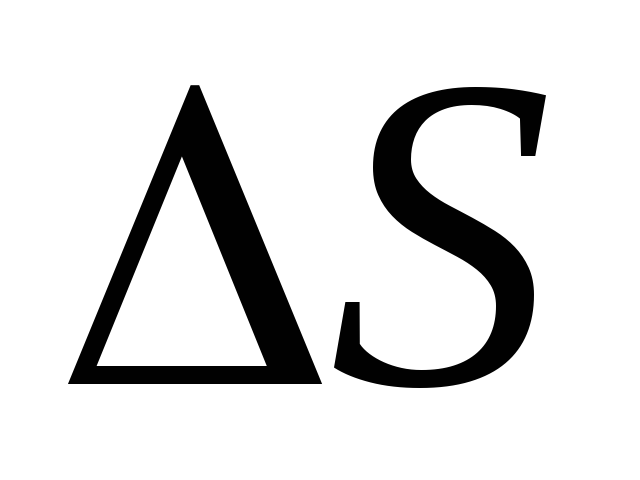

, расположенными относительно плоскости симметрично. Применим к этой поверхности теорему Гаусса

. Поток через боковую часть поверхности будет отсутствовать, так как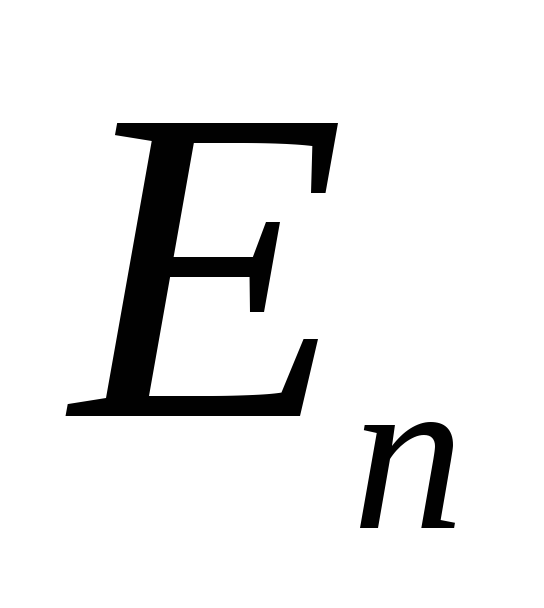в каждой ее точке равна нулю. Для оснований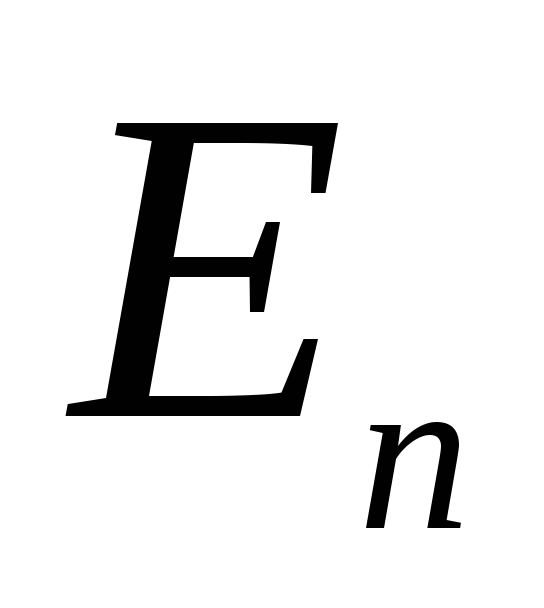совпадает с . Следовательно, суммарный поток через поверхность будет равен

. Внутри поверхности заключен заряд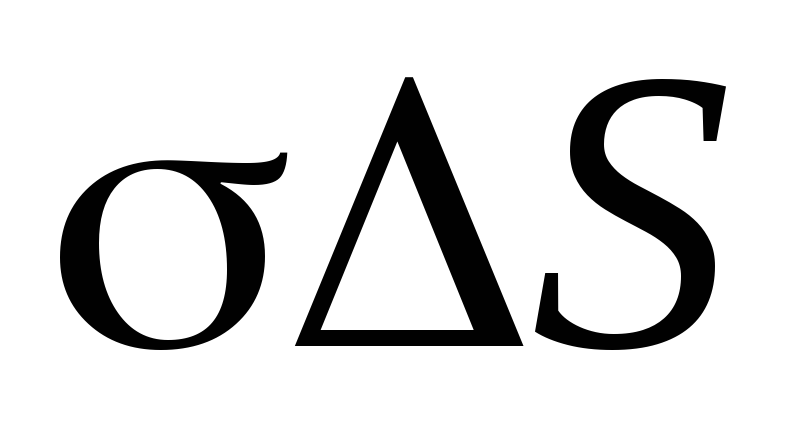

. Согласно теореме Гаусса, должно выполняться условие:

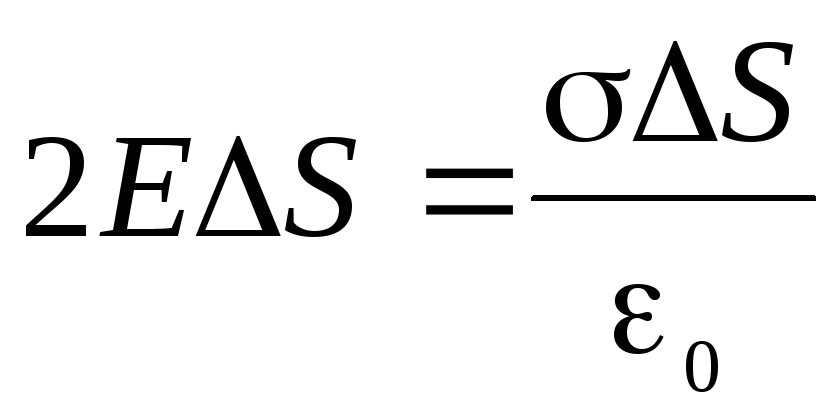, откуда

. (3)

Полученный результат не зависит от длины цилиндра, т.е. на любых расстояниях от плоскости напряженность поля одинакова по величине. Картина линий напряженности выглядит, как показано на рис. 2.11. Для отрицательно заряженной плоскости направления векторов изменятся на обратные. Если плоскость конечных размеров, то полученный результат будет справедлив лишь для точек, расстояние которых от края пластины значительно превышает расстояние от самой пластинки (рис. 2.12).

1. Поле, образованное двумя разноименными заряженными плоскостями (бесконечно большими)

Поле двух параллельных бесконечно больших плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью можно рассматривать как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис.2.13) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

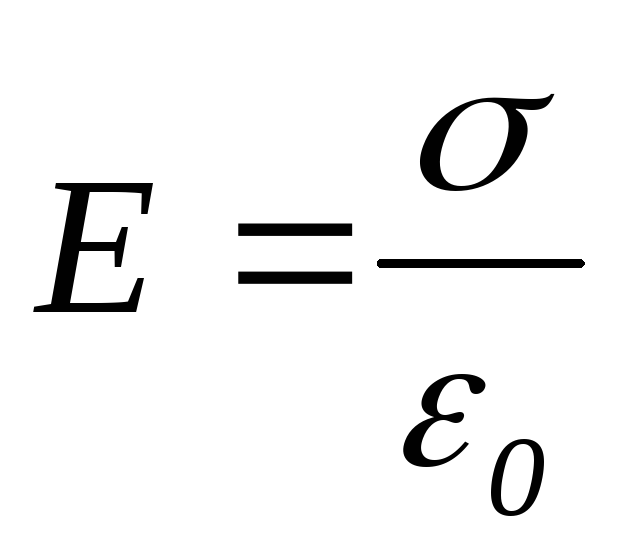
(4)

Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулюE =0 . Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими свойствами, называетсяоднородным . Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых.

Полученный результат приблизительно справедлив и в случае плоскостей конечных размеров, если расстояние между плоскостями значительно меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности напряженности наблюдаются только вблизи краев пластин (рис. 2.14).

Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ .

Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей

Вне плоскостей напряженность поля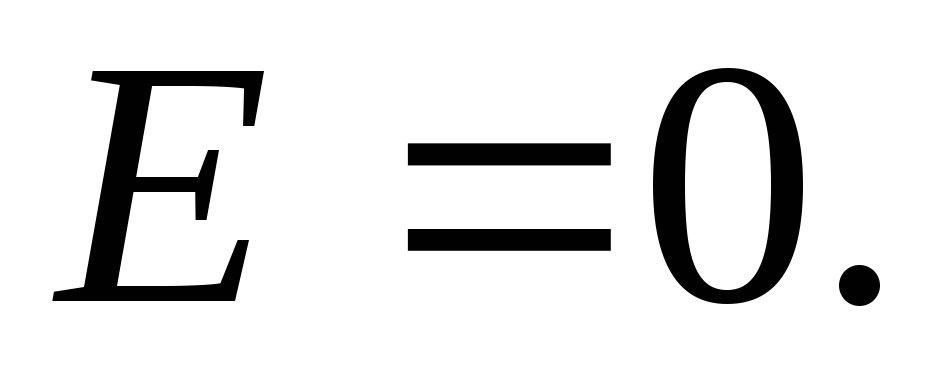

.

Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке.

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):

, т.е.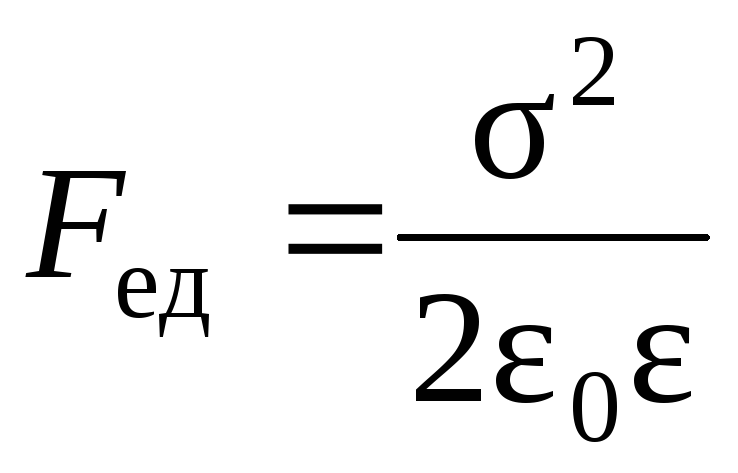

.

Механические силы, действующие между заряженными телами, называют пондермоторными.

Тогда сила притяжения между пластинами конденсатора:

где S – площадь обкладок конденсатора. Т.к.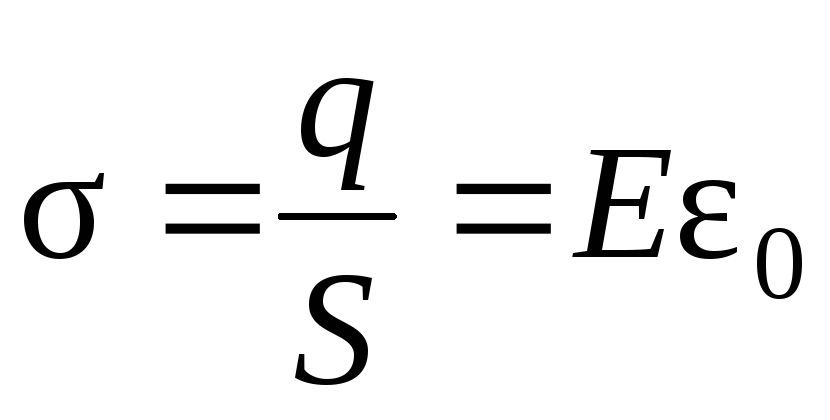

, то

.

Это формула для расчета пондермоторной силы.