Напряженность равномерно заряженной плоскости. Поле равномерно заряженной бесконечной плоскости. Магнитное поле в центре
Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме
1. Поле равномерно заряженной бесконечной плоскости
. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью - заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от вее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны пиниям напряженности (cosα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Еn
совпадает с Е),
т. е. равен 2ЕS.
Заряд, заключенный внутри построенной цилиндрической поверхности, равен .
Согласно теореме Гаусса (81.2), ![]() , откуда
, откуда
Разложим полный поток в сумме парциальных течений через основания и боковую поверхность, и получим, что последнее будет нулевым, так как электрическое поле касается поверхности. 
А так как плотность поверхностного заряда в плоскости постоянна, мы будем иметь. Теперь мы введем понятие. Эта концепция аналогична концепции гравитационного поля, изученной в механике Ньютона.
Аналогичные рассуждения сделаны в электрических полях. С той разницей, что на карту поставлена не масса, а электрический заряд. Они не принимают дискретных значений, а являются целыми кратными элементарному заряду. Поэтому он пропорционален его электрохимическому эквиваленту, определяемому его атомным весом, деленным на валентность. Все эксперименты пришли к такому же выводу, что заряд представляет собой целое число, кратное элементарному заряду, и его значение было определено с большей или меньшей точностью в каждом из них.
Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

Рис. 126
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и -σ. Поле таких плоскостей найдемкак суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние - от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг Другу), поэтому здесь напряженность поля £=0. В области между плоскостями Е=Е + +Е-. (Е + и Е - определяются по формуле (82.1)), поэтому результирующая напряженность
Это значение заряда электрона и заряда протона. Поэтому для изучения электрического поля, генерируемого любым зарядом, мы будем использовать второй груз, намного меньший, чем первый. Тогда мы будем более точно. Соединяя уравнения, и нам придется. Как мы обсуждали ранее, Электрическая сила является вектором.
Расчет электрического поля в любой точке р за счет заряда определяется уравнением. Особенно важным является случай, когда у нас есть 2 заряда одного и того же значения, но противоположных сигналов, разделенных расстоянием 2а. Эта система называется электрическим диполем. Затем мы можем переписать уравнение для. Заметим, что в диполе поле уменьшается с кубом расстояния, а не с квадратом, как в случае изолированного заряда.
Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю.
Рис. 127
3. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q, заряжена равномерно споверхностной плотностью +δ. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиуса г, имеющую общий центр с заряженной сферой. Если г>R , то внутрь поверхности попадает весь зарядQ, создающий рассматриваемое поле, и, по теореме Гаусса (81.2), , откуда
Другая интересная ситуация - заряженное кольцо. Получив кольцо равномерно заряженным, мы вычислим электрическое поле в точке р, расположенной на расстоянии х от центра кольца. Для этого анализа мы будем использовать понятия дифференциального и интегрального.
Чтобы получить полученное электрическое поле в р, мы должны интегрировать эффекты всех элементов кольца. Так как поле является вектором, мы будем иметь следующий векторный интеграл. Как мы видели на примере диполя, здесь мы также имеем делецию компоненты векторов.
Мы заключаем, что на расстояниях, много больших радиуса кольца, он ведет себя как точечный заряд. Мы видели, что каждый электрический заряд связан с электрическим полем, которое его окружает. Мы знаем об этом, потому что, анализируя любую точку в этом регионе, размещая тестовую нагрузку, мы обнаруживаем наличие силы в этой точке. Но как «визуализировать» эту область?
При г>R
поле убывает с расстоянием г по такому же закону, как у точечного заряда. График зависимости E от г приведен на рис. 129. Если г"


Когда мы распространяем железные опилки над магнитным полем постоянного магнита, мы видим выравнивание нити в направлении поля, концентрируясь на более интенсивных участках поля. Он был вдохновлен железными заявками, что Фарадей представил концепцию линий напряженности поля.
Линия силы определяется как касательная кривая в каждой точке к направлению поля в этой точке. Таким образом, с учетом силовой линии легко определить направление электрического поля в каждой точке, так как оно будет касательной к кривой. В дополнение к направлению силовые линии также дают нам направление поля в точке, обозначенное его ориентацией. Только интенсивность не может быть определена. Но, анализируя плотность линий в данной точке, мы будем иметь представление о регионах, поля которых более или менее интенсивные.
Рис. 128 Рис. 129
4. Поле объемно заряженного шара.
Шар радиуса R с
общим зарядом Q,
заряжен равномерно с объемной плотностью р
( -
заряд, приходящийся на единицу объема). Учитывая соображения симметрии (см. п. 3),
можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса г"![]() ,
получаем
,
получаем
Как мы видели ранее, есть положительные и отрицательные сборы. Мы согласны с тем, что линии силы точечного заряда будут иметь радиальное направление, указывающее на «вне», если оно положительно или «внутри», если оно отрицательно. Учитывая это, каковы были бы линии силы нашего Электрического Диполя, изученные в предыдущем пункте? По мере привлечения положительных и отрицательных зарядов силовые линии, «выходящие» из положительного заряда, отвечают линиям, которые «вводят» отрицательный заряд. Схематически это будет выглядеть следующим образом.
![]() (82.4)
(82.4)
Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (82.3), а внутри его изменяется линейно с расстоянием г. согласно выражению (82.4). График зависимости Е от г для рассмотренного случая приведен на рис. 130.
Теорема Гаусса для вектора
Вышеприведенный рисунок, например, следует переосмыслить, вращая вокруг оси, соединяющей две нагрузки. Например, силовые линии положительного заряда, например, будут представлены на рисунке ниже. Важно распознать оси симметрии задачи, поскольку это позволяет нам предсказать симметрию силовых линий. Это будет очень полезно для нас в следующем исследовании электрического потока и закона Гаусса. В случае вышеприведенного рисунка заряженной сферы силовые линии являются радиальными и, следовательно, сферической симметрии.
Теперь представьте себе, например, заряженную плоскость. Мы будем иметь плоскую симметрию с силовыми линиями, параллельными друг другу и перпендикулярными плоскости. Обратите внимание, что направление линий выше и ниже плоскости противоположно. В заряженном цилиндрическом проводе мы будем иметь радиальную симметрию с радиальными силовыми линиями в плоскостях, перпендикулярных проволоке.
![]()
может быть успешно использована как эффективный инструмент расчета напряженности и потенциала электрического поля некоторого распределения заряда, когда стоящий слева интеграл может быть превращен в произведение площади поверхности, по которой производится интегрирование, на величину нормальной к поверхности составляющей вектора , то есть когда
Адриано Лима Барбоса Миранда Директор по корпоративному образованию и новым проектам. Фабиано Прадо Маркес Академический директор - Школа инженерии и технологий. Международная университетская сеть лауреатов. Барни Вилела Генеральный координатор ядра координационной дистанции Катарина де Сена Пиньейру Директор Школы инженерных наук и точных наук.
Его влияние варьируется от объединения атомов и молекул, которые составляют все вокруг нас, до тех потрясений, которые мы чувствуем, когда касаемся какого-то металлического предмета в сухие дни или после протирания воздушно-воздушного шара в нашей блузке и игры на волосах. Все эти явления происходят из-за существования того, что мы называем электрическим зарядом. Но что такое электрический заряд? Каковы его характеристики? С этого момента мы это увидим.
![]() .
.
Вполне очевидно, что для расчета вектора этого будет достаточно, во-первых, когда вектор перпендикулярен поверхности. Следовательно, поверхность интегрирования должна быть эквипотенциальной поверхностью рассчитываемого поля. Её форму надо знать заранее . Наконец, во-вторых, во всех точках этой - эквипотенциальной - поверхности нормальная к ней составляющая должна иметь одну и ту же величину, в противном случае, её нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение . Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что
Рисунок 1 - Некоторые янтарные камни. На греческом языке «янтарь» называется «электрон», слово, которое порождает имя электрона. Электроны, такие как протоны и нейтроны, представляют собой частицы, которые составляют атомы. Многие ученые внесли свой вклад в построение концепции электрического заряда. Сегодня мы знаем, что электрический заряд является одним из фундаментальных свойств частиц. Например, в процессе электризации электроны переносятся из одного тела в другое, оставляя тела электрифицированными с определенным количеством электрического заряда.
![]()
вовсе не вытекает, что и
в точках этой поверхности. Забегая вперед, укажем, что, например, поверхность заряженного проводника при условии равновесного распределения заряда на нем всегда эквипотенциальна, но, если это не шар, а тело сложной формы, то в окрестности выступов (острий) напряженность поля может быть на порядки больше, чем в окрестности впадин на поверхности. Требование постоянства - отдельное требование.
Созвано, что электроны имеют отрицательный заряд, протоны - положительный заряд. В Международной системе символ С представляет собой единицу электрического заряда. Рисунок 2 - Притяжение между нагрузками. Рисунок 3 - Контактный процесс электрификации.
На предыдущем рисунке, в, мы видим, что положительно электрифицированное тело А, находясь в контакте с нейтральным телом В, получает от него электроны, оставляя тело В заряженным положительно. Эксперимент, в котором используются явления электрификации и отталкивания между равными зарядами, - это генератор Ван де Граафа, известный тем, что его используют для того, чтобы вздрогнуть волосы человека, который его касается.
Из сказанного выше вытекает, что теорема Гаусса в состоянии быстро и просто привести к результату (вектору ) лишь в том случае, когда создающее поле распределение заряда обладает высокой степенью симметрии, соответственно, заранее известна форма эквипотенциальных поверхностей поля и есть уверенность в том, что на этих поверхностях. Если всё это имеет место, то решение выглядит следующим простым образом:
Можете ли вы теперь понять, почему мы могли бы использовать полный шар для привлечения волос? Например, когда мы втираем его в кусок шерсти, происходит поток электрических зарядов из шерсти на баллон. Когда мы приближаемся к воздушному шару нитей волос, он в конечном итоге привлекает провода, так как они также имеют электрические заряды внутри. Этот процесс очень похож на то, что вы видели на предыдущем рисунке.
Ниже приведена классификация материалов в отношении проводимости электрических зарядов. Эти материалы называются проводниками. Материалы, которые не имеют этого средства, называются изоляторами или диэлектриками. Материалами, которые имеют промежуточные характеристики, являются полупроводники, широко используемые в электронной промышленности. Металлы, в общем, являются хорошими проводниками, потому что их атомные связи позволяют им иметь много электронов, которые могут свободно перемещаться внутри них, в то время как материалы, такие как стекло, пластик, резина и древесина, имеют электроны, которые гораздо больше связаны с атомами, что делает их хорошей изоляцией при нормальных условиях.
|
|
Сферическая симметрия
Это объясняет, почему провода электрических соединений имеют металлическую часть внутри и пластиковую крышку вокруг них, так что электрические заряды не пересекают материал. В противном случае мы будем чувствовать себя электрическим током каждый раз, когда мы попадаем на электрифицированную проводку. Возможно, вы почувствовали этот эффект, когда пытались настроить антенну телевизора металлической частью, будучи босиком на полу. Вот еще один важный эффект, связанный с электрификацией проводящих материалов.
Обратите внимание на следующий рисунок: нейтральная сфера имеет равное количество положительных и отрицательных зарядов. Электроны перераспределяются при приближении заряженного стержня. Некоторые электроны оставляют шарик заземленным проводником. Чрезмерный положительный заряд распределяется неравномерно.
При сферически симметричном распределении заряда поле, создаваемое им, также сферически симметрично. Векторные (и скалярные) поля с такой симметрией принято также называть центральными полями . Центрально симметричное поле в общем случае можно записать в виде
Здесь - радиус-вектор, начинающийся в центре симметрии поля r - его модуль, - радиальная составляющая напряженности поля, зависящая только от расстояния до его центра симметрии. Потенциал такого поля зависит только от и
Оставшиеся электроны распределены равномерно, и существует однородная сеть распределения положительных зарядов на сфере. Источник: Адаптировано из Сервей и Джуветт. Мы видим, что в нейтральной проводящей сфере содержится такое же количество положительных и отрицательных зарядов. Когда мы приближаемся к отрицательно заряженному стержню из нейтральной сферы, не касаясь его, как и в, происходит процесс поляризации. То есть обвинения отделяются в сфере. Это связано с тем, что положительные заряды привлекаются отрицательными зарядами палки, а негативы отталкиваются.
|
|
И, кроме того, как следует из, при произвольной нормировке потенциал поля имеет вид
Таким образом, условия применимости выполнены и мы можем воспользоваться этим соотношением.
В процессе индукции электрифицированная палочка не касается нейтральной сферы, то есть нет передачи зарядов между палкой и мячиком. До сих пор мы видели некоторые свойства электрических зарядов и форм электрификации. Затем вы изучите, как происходит взаимодействие между электрическими зарядами с количественной точки зрения.
Теперь давайте подробнее рассмотрим, как электрические заряды способны привлекать друг друга. Следуйте схеме кулоновского эксперимента на рисунке. Сфера с отрицательным зарядом притягивает сферу с положительным зарядом; положительная сфера движется до тех пор, пока упругие силы в скручивающейся нити не уравновешивают электростатическое притяжение.
Возьмем в качестве эквипотенциальную сферическую поверхность некоторого текущего радиуса r , её площадь . Виду предполагаемой непрерывности распределения заряда, для используем выражение:
![]() .
.
где - объёмная плотность заряда. Опять-таки, учитывая сферическую симметрию распределения заряда - зависит только от , в качестве элемента объёма естественно взять бесконечно тонкий сферический слой с внутренним радиусом и внешним радиусом . Объём такого слоя , в результате получаем
 .
.
Окончательно, для любого сферически симметричного распределения заряда, когда , получаем
|
|
Продолжение вычислений требует конкретизации вида зависимости плотности заряда от модуля радиус-вектора .
Поле однородно по объёму заряженного шара
Равномерное по объёму шара радиуса распределение заряда (рис. 1.41) означает, что его плотность заряда имеет вид


Рис. 1.41. Силовые линии электрического поля однородно заряженного шара
Не следует забывать, что по условию вне шара зарядов нет.
Поскольку в точке плотность заряда меняется скачком: предел «слева» отличен от нуля ![]() , а предел «справа» равен нулю
, а предел «справа» равен нулю ![]() , вычисление придется проводить в два этапа: сначала для сферической поверхности радиуса (она лежит внутри шара), а потом для сферической поверхности радиуса (она охватывает шар). В первом случае
, вычисление придется проводить в два этапа: сначала для сферической поверхности радиуса (она лежит внутри шара), а потом для сферической поверхности радиуса (она охватывает шар). В первом случае
 .
.
Соответственно, поле
|
|
растет линейно с ростом расстояния до центра шара, что объясняется просто: площадь поверхности , а заряд внутри неё
Во втором случае интеграл «обрезается сверху» при :

В последнем выражении учтено, что , где - полный заряд шара. Таким образом, вне шара его поле есть поле точечного заряда равного полному заряду шара и помещенного в центр этого шара:
 .
.
Оба выражения можно объединить в одну формулу. Если использовать полный заряд шара , получим:
|
|
Если вместо полного заряда шара использовать в качестве параметр плотность заряда , эти формулы приобретут следующий вид (рис. 1.42):
|
|

Рис. 1.42. Распределение напряженности электрического поля однородно заряженного шара
Формулы и выражают одну и ту же зависимость, их удобство определяется тем, какие параметры заданы: или . Из этих формул наглядно видно, что на поверхности шара напряженность поля непрерывна, то есть не имеет разрыва. Это обусловлено тем, что в данном случае разрыв плотности заряда на поверхности шара первого рода - конечной величины: с на нуль. Поэтому, как в, так и в в верхней и в нижней формулах поставлены знаки нестрогих неравенств. В каких случаях напряженность поля может терпеть разрыв, будет ясно из следующего примера.
Потенциал поля легко найти, подставив, например, из в и выполнив интегрирование. Получаем:
|
|
где и - постоянные интегрирования, которые находятся из следующих соображений. Константа определяется из условия нормировки, например, на нуль на бесконечности

Откуда . Константа определяется из условия непрерывности потенциала на поверхности шара, то есть при :
|
|


Отметим, что требование непрерывности потенциала нередко называют «сшивкой» двух решений на границе раздела. В данном случае это граница раздела двух областей: областью, где есть заряд (внутри шара), и областью, где его нет (вне шара). Уже сейчас можно отметить, что потенциал непрерывен во всех случаях, кроме одного: так называемого «двойного слоя». Представьте поверхность, по одной стороне которой с плотностью распределен положительный заряд, а по другой стороне которой с плотностью распределен отрицательный заряд. Такая поверхность и называется двойным слоем, на этой поверхности потенциал терпит разрыв. Такую (плоскую) поверхность можно получить, неограниченно сближая две обкладки плоского конденсатора. То же самое можно проделать для конденсатора любой формы, например, сферического или цилиндрического. Во всех остальных случаях потенциал непрерывен.
Подставляя полученные значения констант интегрирования в, запишем окончательный результат в виде
|
|
При такой нормировке потенциал в центре шара отличен от нуля и равен
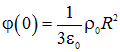 .
.
Полученные результаты иллюстрирует приведенный ниже рисунок 1.43.
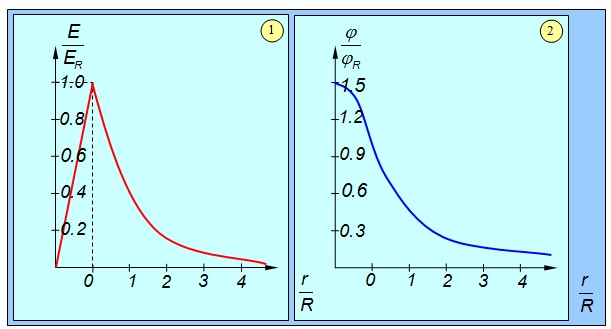
Рис. 1.43. Напряженность (1) и потенциал (2) электрического поля равномерно заряженного шара радиусом R в единицах напряженности и потенциала на его поверхности (r = R)
Поле равномерно заряженной сферической поверхности
В данном случае равномерного распределения заряда по сферической поверхности, как и в предыдущем, имеет место сферическая симметрия, поэтому общие формулы, полученные выше, применимы и здесь. Однако относиться к ним необходимо с известной осторожностью по следующей причине. Входящая в правую часть объемная плотность заряда ведет себя в данном случае следующим интересным образом:


Рис. 1.44. Напряженность электрического поля равномерно заряженной сферы
Действительно, заряд имеется только на поверхности , то есть при , всюду внутри, то есть при и всюду снаружи, то есть при зарядов нет. То, что объемная плотность заряда в точках поверхности обращается в бесконечность (+∞ в случае положительного заряда и –∞ в случае отрицательного) можно показать следующим образом. На рисунке рядом изображен участок некоторой поверхности, по которой с поверхностной плотностью распределен заряд. Для определения величины объёмной плотности заряда в некоторой точке поверхности рассмотрим цилиндр (рис. 1.45), верхнее основание которого находится над поверхностью, а нижнее - под поверхностью. Площадь оснований цилиндра равна , высота - , объём . Заряд внутри цилиндра , объёмная плотность заряда по определению равна пределу отношения заряда, находящегося внутри некоторого объема, к величине этого объема при стремлении последнего к нулю (со всеми оговорками относительно объёма «физически бесконечно малого»). Получаем
![]()

Рис. 1.45. Плотность заряда на поверхности
Важно, что плотность на поверхности равна бесконечности. Функции такого рода (везде, кроме одной точки - нуль, а в этой единственной точке - бесконечность) относятся к классу так называемых обобщенных функций, называются функциями Дирака в честь физика Дирака, впервые введшего в обиход физики такую функцию для удовлетворения нужд квантовой механики. Мы не будем здесь подробно исследовать и использовать в расчетах такого рода функции. Наша цель показать, что рассмотрение формально бесконечно тонких заряженных поверхностей приводит к появлению у объёмной плотности заряда разрывов (бесконечных), что, в свою очередь, порождает бесконечные разрывы на такой заряженной поверхности у напряженности электрического поля. Подчеркнем, что потенциал поля при этом остается непрерывным.
Выход из положения прост. При всех используем первую из формул с , получаем, что всюду внутри однородно заряженной сферической оболочки поле отсутствует: . При всех справедлива вторая формула из. Как и в случае однородно по объёму заряженного шара, вне однородно заряженной сферической оболочки, её поле есть поле точечного заряда, помещенного в центр этой оболочки и равного её полному заряду. В данном случае, разумеется .
Окончательный результат такой:
|
|
На самой сферической поверхности напряженность поля в этом случае терпит разрыв. Зависимость радиальной компоненты поля от расстояния до центра сферической поверхности показана на рис. 1.46.

Рис. 1.46. Зависимость поля от расстояния до центра сферической оболочки
Зависимость потенциала от расстояния до центра сферической оболочки можно получить, интегрируя. При нормировке на нуль на бесконечности результат выглядит следующим образом:
|
|
Зависимость показана на рис. 1.47.

Рис. 1.47. Потенциал равномерно заряженной сферы
Однородное (равномерное) распределение заряда по бесконечно длинной цилиндрической поверхности (рис. 1.48) обладает цилиндрической, трансляционной и зеркальной симметрией. Это означает следующее. При повороте такого распределения заряда вокруг оси цилиндрической поверхности на любой угол оно совпадает само с собой. При сдвиге (переносе, трансляции) такого распределения заряда на любое расстояние вдоль оси симметрии оно также совпадает само с собой. И, наконец, если через любую точку на оси симметрии провести плоскость перпендикулярную к оси, и отразить в этой плоскости как в зеркале «верхнюю» часть распределения заряда, то отражение «верхней» части совпадет с «нижней» и наоборот, отражение «нижней» совпадет с «верхней». Другими словами, это распределение заряда инвариантно относительно указанных преобразований. Следовательно, и создаваемое этим распределением заряда электрическое поле должно быть инвариантно (совпадать само с собой) при указанных преобразованиях.

Рис. 1.48. Бесконечно длинная цилиндрическая поверхность
Введем цилиндрическую систему координат: ось направим по оси симметрии, - расстояние до оси симметрии, - азимутальный угол, угол поворота вокруг оси симметрии, - по-прежнему потенциал поля.
Из свойств симметрии вытекает, что потенциал поля не может зависеть ни от координаты - нарушится трансляционная симметрия, ни от координаты - нарушится осевая (цилиндрическая) симметрия. Остается только зависимость от - расстояния до оси цилиндра. Таким образом:
Соответственно
|
|
вектор напряженности электрического поля направлен по радиальным прямым, перпендикулярным оси симметрии (рис. 1.49), и его величина зависит только от расстояния до оси. Потенциальные поверхности представляют собой цилиндры соосные с заряженной цилиндрической поверхностью.

Рис. 1.49. Вектор напряженности электрического поля направлен по радиальным прямым
Используя эти обстоятельства, будем интегрировать в левой части теоремы Гаусса по замкнутой поверхности цилиндра с радиусом основания и высотой , соосного с рассматриваемой, заряженной цилиндрической поверхностью радиуса . Поток через основания цилиндра равен нулю ввиду того, что на основаниях , а поток через его боковую поверхность равен произведению на её площадь: . Соответственно, суммарный (через всю замкнутую поверхность рассматриваемого цилиндра) поток вектора равен
При , находящийся внутри цилиндра заряд, равен
![]()
где - линейная плотность заряда численно равная заряду, приходящемуся на единицу длины цилиндрической поверхности. Согласно теореме Гаусса

откуда для получаем
При внутри цилиндра, через поверхность которого вычисляется поток вектора , зарядов нет, и потому поле равно нулю. Объединяя эти два результата, получаем окончательно (рис. 1.50):
|
|
Ввиду поверхностного характера распределения заряда (см. подробнее предыдущий расчёт) на самой заряженной поверхности, то есть при радиальная компонента поля терпит разрыв.

Рис. 1.50. Напряженность электрического поля равномерно заряженной цилиндрической поверхности
Интегрирование (1.51) (см. также (1.49)), требование непрерывности потенциала при , и нормировка , приводят к следующей зависимости потенциала от расстояния до оси цилиндрической поверхности:
|
|
В данном случае, когда бесконечно большой по модулю заряд распределен по бесконечно длинному цилиндру, относится к тем случаям, когда нормировка на нуль на бесконечности лишена смысла. Как видно из (1.52), зависимость потенциала от расстояния до оси логарифмическая, нормировка на нуль на бесконечности, на языке формул (1.52), означает, что , но, тогда потенциал будет бесконечно большим по модулю на любом конечном расстоянии от оси заряженной поверхности, что лишено смысла. Выбор того конечного расстояния от оси симметрии, на котором удобно потенциал считать равным нулю трудностей не вызывает и обусловлен спецификой задачи. Например, ничто не мешает положить , тогда потенциал всюду внутри и на самой заряженной поверхности будет равен нулю.
Поле бесконечной равномерно заряженной плоскости
Пусть поверхностная плотность заряда равна ![]() . Такое распределение заряда по бесконечной плоскости характеризуется тем, что его вид не зависит от: а) поворота на любой угол вокруг любой оси перпендикулярной плоскости, б) сдвига на любое расстояние вдоль прямой лежащей в плоскости и любого направления. Наконец, в) отражение данного распределения заряда в зеркале, совпадающем с самой плоскостью, оставит его неизменным.
. Такое распределение заряда по бесконечной плоскости характеризуется тем, что его вид не зависит от: а) поворота на любой угол вокруг любой оси перпендикулярной плоскости, б) сдвига на любое расстояние вдоль прямой лежащей в плоскости и любого направления. Наконец, в) отражение данного распределения заряда в зеркале, совпадающем с самой плоскостью, оставит его неизменным.
Из анализа симметрии достаточно очевидно, что потенциал в любой точке вне плоскости может зависеть только от расстояния от этой точки до плоскости. Направим ось декартовой системы координат перпендикулярно плоскости, а оси и пусть принадлежат самой плоскости, тогда
|
|
Причем, в силу зеркальной симметрии, поле «перед» плоскостью отличается от поля «за» плоскостью только направлением вектора . Это означает, что зависимость от должна быть нечетной, а зависимость потенциала от должна быть четной.
В силу этих соображений возьмём замкнутую поверхность - ту, для которой будем писать теорему Гаусса, - следующего вида (рис 1.51).

Рис. 1.51. Электрическое поле заряженной плоскости
Это цилиндр с боковой поверхностью перпендикулярной плоскости и с основаниями параллельными плоскости. Высота цилиндра , площадь оснований . Учитывая нечетность зависимости , основания цилиндра удобно расположить на одинаковом расстоянии от плоскости, тогда вклад оснований в поток будет одинаков. Напряженность поля на основаниях, во-первых, им перпендикулярна, во-вторых, сонаправлена с внешней нормалью, в-третьих, она одинакова во всех их точках по абсолютной величине
![]()
Вклад в поток вектора от боковой поверхности равен нулю, так как на боковой поверхности .
Поэтому полный поток через всю замкнутую цилиндрическую поверхность равен
Внутри рассматриваемой цилиндрической поверхности находится заряд
где - плотность заряда на плоскости. По теореме Гаусса
следовательно, модуль напряженности поля заряженной плоскости равен
Подчеркнём, что результат очевидным образом не зависит от того, на каком расстоянии от плоскости расположены основания рассмотренного цилиндра. Отсюда следует, что с каждой стороны от плоскости создаваемое ею электрическое поле однородно.
Используя введенную ранее ось перпендикулярную заряженной плоскости, поле с обеих сторон от плоскости можно описать одной формулой, пригодной при любом знаке заряда на плоскости
Здесь - орт оси .
Интегрируя с учетом
для зависимости от потенциала поля плоскости нетрудно получить:
|
|
Потенциал в нормирован условием . Здесь, как и в примере с бесконечно длинной заряженной цилиндрической поверхностью, потенциал растет при удалении на бесконечность, поэтому нормировка на нуль на бесконечности лишена смысла.
Силовые линии поля заряженной плоскости показаны на рис. 1.52 и 1.53.

Рис. 1.52. Поле положительно заряженной плоскости
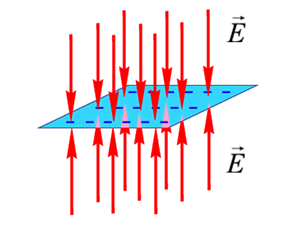
Рис. 1.53. Поле отрицательно заряженной плоскости
Поле плоского конденсатора
Определим напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными однородно и разноименно. Плотности заряда на плоскостях по модулю одинаковы и равны, соответственно: и (идеальный плоский конденсатор). С помощью рис. 1.54 нетрудно сообразить, что в зазоре между плоскостями, создаваемые ими поля направлены в одну сторону, поэтому внутри суммарное поле в два раза больше поля от каждой из плоскостей. Снаружи от плоскостей создаваемые ими поля направлены в противоположные стороны, соответственно, суммарное поле от обеих плоскостей равно нулю (рис. 1.55).
|
|

Рис. 1.54. Электрическое поле плоского конденсатора

Рис. 1.55. Электрическое поле разноименно заряженных плоскостей
|
|

В Дополнении 6 разобран пример с движением заряженной частицы в постоянном электрическом поле.
Потенциал поля заряженного диска
Как уже не раз отмечалось, зная потенциал поля точечного заряда и используя принцип суперпозиции, в принципе всегда, можно вычислить потенциал поля, создаваемого любым распределением зарядов.
Найдем для примера потенциал электрического поля, создаваемого на оси тонкого диска радиуса R , равномерно заряженного с поверхностной плотностью заряда (рис. 1.57). В силу осевой симметрии в точках на оси две перпендикулярных к оси составляющих напряженности поля равны нулю: , остается найти - составляющую поля, направленную вдоль оси.
Можно разложить в ряд, ограничившись первыми двумя членами разложения
Закон Кулона и размерность пространства
Пространство, в котором мы живем, имеет три измерения. Иными словами, нужны три координаты (например, в декартовой или в сферической системах) для задания положения точки А (рис. 1.58). Оказывается, число 3 тесно связано с формой закона Кулона. Мы видели, что теорема Остроградского - Гаусса следует из закона Кулона. Верно и обратное, закон Кулона можно вывести из теоремы Остроградского - Гаусса. Но эта теорема носит более общий характер, чем закон Кулона. В частности, она применима к пространствам с размерностью , где не обязательно должно быть равно трем.
Так, в двумерном пространстве роль объема играет наша площадь. Действительно, сфера - это геометрическое место точек пространства, равноудаленных от центра. Согласно этому определению, двумерная сфера - это окружность радиусом мерном мире пропорциональна мерном мире.
При получаем отсюда закон обратных квадратов (закон Кулона). При находим На самом деле мы уже знакомы с таким поведением электрического поля. Именно такой закон (10.17) мы вывели для поля бесконечного заряженного цилиндра. Если как следует подумать и вспомнить расположение силовых линий цилиндра, то станет ясно, что ничего не зависит от координаты вдоль оси цилиндра. Таким образом, эта система имитирует электрическое поле в двумерном мире. Теперь легче понять, что заряженная плоскость имитирует точечный заряд в одномерном мире: все зависит только от одной координаты - расстояния до плоскости. Но мы нашли выше, что электрическое поле от этого расстояния не зависит. И из формулы (10.49) при также следует, что напряженность grad ) должно дать выражение для напряженности электрического поля.
Отсюда следуют любопытные выводы. Поскольку в одно- и двумерном мирах потенциалы растут на бесконечности, нужна бесконечно большая работа, чтобы развести два притягивающихся заряда. Это означает, что в мирах малой размерности возможно лишь финитное движение двух притягивающихся тел (зарядов, масс). Напомним, что финитным называется движение в ограниченной области пространства. Поэтому в мирах с нельзя ионизировать атом, нельзя запустить спутник за пределы Солнечной системы и т. п. В таком мире не было бы химических реакций, не могли бы эволюционировать галактики и звезды. Словом, жизнь там была бы застойно скучна.
Можно было бы ожидать более приятного времяпрепровождения в многомерных мирах. Увы, и это оказывается иллюзией. Исследование уравнения движения

приводит к выводу, что при в сущности отсутствует финитное движение: оно реализуется только для круговых орбит, да и то является неустойчивым - малейшее возмущение приводит к падению электрона (планеты) на притягивающий центр или его (ее) убеганию на бесконечно большое расстояние. Выходит, в таком мире атомы, планетные системы и все остальное вообще не могло бы образоваться. Никакой стабильности в мирах высшей размерности - вот альтернатива «застойным» маломерным мирам. Только при возможно как устойчивое финитное, так и инфинитное движения. Получается, что трехмерное пространство - единственно удобная форма существования и движения материи, по крайней мере, известных нам ее видов, которые мы изучаем в физике.
Дополнительная информация
http://hea.iki.rssi.ru/~nik/astro/spher.htm - сферическая система координат;
http://edu.ioffe.ru/register/?doc=physica/lect3.ch2.tex - финитное движение, задача Кеплера.