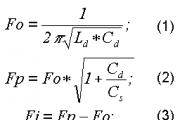Меню ≡ ╳

Практическое занятие. Практическое занятие Потребление и спрос

Все о печах и дымоходах

13.10.2021

Объем потребления некоторого товара домашним хозяйством (q) в зависимости от дохода (I) описьпвается равенством:

Определить, при каких значениях дохода товар для данного домашнего хозяйства является

а) низшим благом;

б) нормальным благом;

в) необходимьм благом;

г) роскошным благом.

ЗАДАЧА № 2

Индивид потребляет два блага в количествах x и y соответственно. Согласуются ли приведенные ниже функции полезности с аксиомами потребительских предпочтений? (да/нет)

а) U(x, y) = yjx2 + y2 ;

в) U(x, y) = - +

ЗАДАЧА № 3

Предпочтения индивида характеризуются предельными нормами замещения MRSxy = 2, MRSxz = 0.8. Найти предельные нормы замещения а) MRS , б) MRS , в) MRS , г) MRS .

А 1 / yx7 / zx7 " yz7 " zy

ЗАДАЧА № 4

Домашнее хозяйство потребляет два блага в количествах x и y; его предпочтения описываются функцией полезности U(x, y). Найти функцию спроса домашнего хозяйства, если

а) U(x, y) = x3y2;

б) U(x, y) = xaye.

ЗАДАЧА № 5

Предпочтения двух индивидов описываются функциями полезности

U-(x, y) = --; U2(x, y) = ln x + ln y ln(x + y).

Различаются ли предпочтения этих индивидов? ЗАДАЧА № 6

Рассмотрим модель, в которой предпочтения потребителя относятся не к продуктам, а к характеристикам, которыми продукты обладают (модель Ланкастера). Допустим, что рассматривается множество продуктов, обладающих двумя характеристиками (X и Y).

Продукт (0

Обозначим (x., y) количественные меры соответствующих характеристик в единице і-го продукта, причем простоты ради в качестве единицы каждого продукта принимается количество продукта, приобретаемое за одну денежную единицу. Будем считать, что предпочтения в пространстве характеристик удовлетворяют тем же аксиомам, что и предпочтения в пространстве благ в традиционной теории.

В таблице (см. выше) приведены данные по шести различным продуктам. Какие из них не имеют перспектив быть проданными на рынке?

ЗАДАЧА № 7

Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его доход I = 60, а предпочтения описываются функцией полезности U(x, y) = xy .

благ pX = 9, pY = 4.

из благ от цен и дохода.

ЗАДАЧА № 8

Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его предпочтения описываются функцией

полезности U(x, y) = л/x + yfy . Известен доход: I = 60.

а) Найти объемы спроса на каждое из благ при ценах

благ pX = 10, pY = 5.

б) Определить зависимости объемов спроса на каждое

из благ от цен и дохода.

в) Определить характер взаимозависимости благ в потреблении.

ЗАДАЧА № 9

Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его предпочтения описываются функцией по1

лезности U(x, y) = y , цены благ равны pX = 16, pY = 25.

x X а) Найти объемы спроса на каждое из благ при значениях дохода I = 70; I = 15.

б) Определить зависимости от дохода объемов спроса на каждое из благ.

ЗАДАЧА № 10

Индивид потребляет два блага, X и Y, в количествах x и y соответственно. Функция полезности индивида: U = ax + by + xy, a > 0, b > 0.

а) Пусть a = 10, b = 25. Определить объемы потребления благ,

если цены благ pX = 5, pY = 2 при доходе индивида I = 200;

б) то же при доходе индивида I = 100;

в) при каких соотношениях дохода и цен оптимум потребителя будет внутренним (x > 0, y > 0)?

ЗАДАЧА № 11

Домашнее хозяйство приобретает благо X, производимое естественной монополией, по цене pX = 10 в количестве x = = 5. Государство, регулирующее цену продукта естественной монополии, сочло целесообразным повысить цену до p"X = = 14 и выплачивать домашнему хозяйству компенсацию в размере (p"X pX) x = 20.

а) Изменилось ли благосостояние домашнего хозяйства,

и если да, то в какую сторону?

б) Проверить утверждение на следующем примере: домашнее хозяйство кроме блага X потребляет еще одно благо, Y, цена которого pY = 1 не изменилась; доход домашнего

хозяйства I = 100, а функция полезности U(x, y) = -Jxy .

ЗАДАЧА № 12

Классификация благ, основанная на кривых Энгеля, учитывает изменения доли дохода, направленной на покупку рассматриваемого блага, в зависимости от изменения дохода. Докажите следующие утверждения:

если доля дохода, направляемая на покупку данного блага, увеличивается с ростом дохода, то эластичность объема потребления по доходу больше единицы;

если доля дохода, направляемая на покупку данного блага, уменьшается с ростом дохода, то эластичность объема потребления по доходу меньше единицы.

ЗАДАЧА № 13

Домашнее хозяйство потребляет три блага, X, Y и Z. Их доли в расходах составляют соответственно sX = 50\%, sY = = 30\%, sZ = 20\%. Известны эластичности по доходу объемов потребления благ X и Y: EI[x] = 2, E^y] = 0.6.

а) Найти эластичность объема потребления блага Z по

б) Определить, к какому типу относится каждое из благ.

ЗАДАЧА № 14

Докажите утверждение: если среди благ, потребляемых домашним хозяйством, есть хотя бы одно низшее, то среди них имеется также хотя бы одно роскошное.

ЗАДАЧА № 15

Телефонная компания предлагает потребителям услуг на выбор два варианта тарифов: (а) 4 ед./мин без абонентской платы; (б) 2 ед./мин и абонентская плата 20 ед. Какой из тарифов выберет каждый из следующих потребителей:

функция полезности U1 = x0.5y0.5, доход 11 = 100 ед.;

функция полезности U2 = x0.25y0.75, доход 12 = 100 ед.;

функция полезности U3 = x0.25y0.75, доход I = 200 ед. Здесь x - количество (в минутах) потребляемых услуг

телефонной компании, y - объем потребления всех других благ, цена которых равна 1 ед.

2.2 РЕШЕНИЯ

РЕШЕНИЕ ЗАДАЧИ № 1

Из графика видно, что с ростом дохода от нуля до некоторого уровня объем потребления товара возрастает, так что благо является нормальным; при дальнейшем росте дохода данный товар вытесняется некоторым заменителем, объем его потребления снижается и товар становится низшим.

Найдем границы области возрастания объема потребления;

для этого продифференцируем объем потребления по доходу:

dq = _ 2I (I +10)8 8I2(I +10)2 = _ 20I -12

dI (I +10)6 (I +10)4.

Производная обращается в нуль при I = 20; при меньших значениях дохода производная положительна, и объем возрастает, при больших - убывает. Таким образом, товар является нормальным при I < 20 и низшим - при I > 20.

Для того чтобы выяснить, при каких уровнях дохода товар является необходимым благом, а при каких - роскошным, целесообразно воспользоваться эластичностью объема потребления по доходу: 1 q dl I +10

Для роскошного блага эластичность объема потребления по доходу больше единицы. Последнее равенство показывает, что EI[q] > 1 при 0 < I < 5. Если 5 < I < 20, то потребление растет с доходом, но медленнее, чем доход, BI[q] < 1, и рассматриваемый товар является необходимым благом.

Итак, рассматриваемый товар является низшим благом при I > 20 и нормальным - при I < 20; при 0 < I < 5 он является роскошным благом, при 5 < I < 20 - необходимым.

Комментарии.

Знак производной всегда совпадает со знаком эластичности. Поэтому ответы на все вопросы задачи можно было получить, рассматривая диапазоны уровней дохода, в пределах которых значения BI[q] превышают единицу, лежат между нулем и единицей и оказываются отрицательными.

Современная классификация потребляемых благ берет начало с исследований Э. Энгеля, выполненных в середине XIX в. и, естественно, не использовавших понятия эластичности функций. Проанализировав структуру потребительских бюджетов, Энгель установил, что с ростом дохода сумма расходов на питание возрастает, но их доля в распределении дохода падает. Если мы рассматриваем определенный товар, потребляемый в количестве q и покупаемый по цене p (которую мы считаем здесь неизменной), то расходы равны pq. Доля, приходящаяся на данный товар, равна pq/I; если она с ростом дохода убывает, то BI < 0. Воспользовавшись свойствами эластичности (см. Приложение) и учитывая неизменность цены, представим это соотношение в виде BI[q] 1 < 0, или BI[q] < 1. При этом абсолютная сумма расходов возрастает, EI = BI[q] > 0. Таким образом, закон Энгеля применительно к необходимому благу (подобно продуктам питания) формулируется в виде двойного неравенства 0 < EI[q] < 1.

РЕШЕНИЕ ЗАДАЧИ № 2

Аксиомы потребительских предпочтений:

полнота (сопоставимость любых потребительских наборов);

транзитивность;

ненасыщаемость («больше - лучше, чем меньше», предпочтительность набора, содержащего больший объем любого блага без уменьшения объемов остальных);

непрерывность;

выпуклость множества наборов, предпочтительных по отношению к любому данному.

Если система предпочтений потребителя задана функцией полезности, то аксиомы 1 и 2 тем самым выполняются. Аксиома 4 выполняется, если функция полезности непрерывна. Во всех вариантах а) - в) функции полезности непрерывны, так что требования аксиом 1, 2 и 4 можно считать выполненными.

Аксиома 3 выполняется, если функция полезности возрастает по каждому аргументу. Функция варианта а), очевидно, удовлетворяет этому требованию, варианта в) - нет, она является убывающей по каждому аргументу. Так как

т. е. значения функций б) и в) - взаимно обратные величины, функция б) является возрастающей (в чем можно убедиться и любым иным способом).

Аксиома 5 требует, чтобы каждая кривая безразличия

ограничивала снизу выпуклую область. Это означает, что

предельная норма замены MRS должна убывать с ростом

x и возрастать с ростом y. Функция а) этому требованию не

отвечает: соответствующие кривые безразличия - 90-градусные дуги окружностей с центром в начале координат.

Для функции б) ^ ^2 ґ 2

dU / dx = -2- I ; dU / dy =

так что 2 MRS ==Udx = (У1 .

Таким образом, функция б) удовлетворяет всем аксиомам предпочтений. Ответ:

а) нет; б) да; в) нет. РЕШЕНИЕ ЗАДАЧИ № 3

Если единица блага x замещается a единицами блага y с сохранением уровня полезности, то единица блага y замещается 1/a единицами блага x. Поэтому MRS = 1/MRS .

Если к тому же единица блага y замещается b единицами блага z при том же условии, то единица блага x замещается ab единицами блага z и поэтому

MRS MRS = MRS .

Это позволяет найти все неизвестные предельные нормы замещения по известным MRS и MRS .

Комментарий.

Более формализованный подход связывает предельные нормы замены с производными функции полезности:

MRS = Udx и т. п.,

откуда следуют приведенные выше соотношения. Заметим, что система предпочтений определяет функцию полезности неоднозначно: если функция U(x, y, ...) описывает предпочтения данного потребителя, то точно так же их описывает функция U1(x, y, ...) = cp(U(x, y, ...)), где ф - произвольная монотонно возрастающая функция. Но

dU1 / dx = (dp / dU) ■ (dU / dx) = dU / dx

dU1/dy ~ dp / dU) ■ (dU / dy) " dU / dy " так что отношение частных производных зависит не от количественной шкалы, в которой отображаются полезности, а лишь от предпочтений индивида.

а) 0.5; б) 1.25; в) 0.4; г) 2.5.

РЕШЕНИЕ ЗАДАЧИ № 4

а) Прежде всего, определим предельную норму замены

как функцию x и у:

U = 3x2y2; U = 2x3y, отсюда MRS = Ux = 3у.

При ценах благ p , p в точке оптимума потребителя соотношение цен p/p равно предельной норме замены, так что

Заметим, что p x и p у - это расходы потребителя соответственно на первое и второе блага. Отсюда ясно, как данный потребитель распределяет свой бюджет: долю 0.6 своего дохода он должен потратить на покупку первого блага, долю 0.4 - на покупку второго. Если его доход равен I, то объемы спроса на первое и на второе благо равны:

x = 0.6 -; у = 0.4 -.

Каждое из приведенных равенств описывает функцию спроса на соответствующее благо.

б) Те же рассуждения применительно к более общему

случаю приводят к соотношению:

откуда: РуУ Р

а + р px а+р py

Комментарий.

В приведенных задачах объем спроса на каждое благо зависел от дохода и от цены данного блага и не зависел

от цены другого блага, а доля расходов на данное благо в величине дохода зависела только от параметров функции полезности и не зависела ни от дохода, ни от цен.

Постоянство доли расходов (независимость от дохода) означает, что оба блага занимают пограничное положение между необходимыми и роскошными благами. Независимость объема спроса на каждое благо от цены другого блага означает, что блага независимы в потреблении.

Доли расходов на каждое благо зависели не от абсолютных значений параметров а и р, а лишь от их соотношения. Так, решение в п. а) не изменилось бы, если бы показатели степени равнялись не 3 и 2, а, скажем, 15 и 10 или 0.3 и 0.2. Последнее обстоятельство связано с тем, что функции полезности, связанные монотонно возрастающим преобразованием, представляют одну и ту же систему предпочтений (порядковая концепция полезности). Пусть x - вектор, представляющий набор благ, U^x) и U2(x) - функции полезности, причем U2(x) = ф(^1(х)), где ф - монотонно возрастающая функция. В этом случае если ^1(x1) > U^x2), то и U2(x^ > > U2(x2), т. е. набор, оцениваемый функцией U как более предпочтительный, так же оценивается и функцией U2. Возведение в положительную степень - монотонно возрастающее преобразование, и функция х15у10 = (х3у2)5 описывает ту же систему предпочтений, что и функция в задании a). Тот же результат дает и, например, логарифмирование:

U3(x) = 3 ln х + 2 ln y = 1п(х3у2).

В заданиях потребитель ограничивался двумя благами, но выводы остаются справедливыми при произвольном числе благ. Пусть x = (х1, х2, хп) и

Будем использовать обозначения для предельных по-лезностей,

Отсюда получаем выражение для предельных норм замены:

U. a. х. MRS.. = = , U. а.} х.

Полученное выражение позволяет при заданных ценах выразить расходы на все потребляемые блага через расходы на какое-нибудь одно, например первое:

MRS;/ = P = - Х, откуда:

р х\% = -рл. (3)

Теперь бюджетное ограничение можно представить в виде

так что с учетом равенства (2) p1x1 = a17, а равенство (3) показывает, что аналогичные выражения справедливы для всех благ: p.x. = aI. Таким образом, если функция полезности имеет вид (1), то доли расходов на отдельные блага в общей сумме не зависят ни от величины дохода, ни от цен. Они представляют собой постоянные величины, пропорциональные параметрам ai, а если эти параметры нормированы в соответствии с равенством (2), то доли совпадают с параметрами. Объем спроса на каждое благо равен х. = a.I/p..

РЕШЕНИЕ ЗАДАЧИ № 5

Нетрудно заметить, что U1(x, y) = In U2(x, y). Логарифм - возрастающая функция. Если первый потребитель предпочитает набор (х1, y1) набору (х2, y2), т. е. если U1(x1, y1) > U1(x2, y2), то U2(x1, y1) > U2(x2, y2), а это означает, что второй потребитель также предпочитает первый набор второму. В рамках порядковой теории полезности предпочтения потребителей неразличимы.

Комментарии.

По формульной записи функций полезности далеко не всегда легко догадаться, что одна из них является функцией от другой. Но это всегда можно выяснить, сравнив предельные нормы замены: если предельные нормы замены совпадают при любых комбинациях благ, то они выражают одну и ту же систему предпочтений индивидов. При решении задачи 2 определена предельная норма замены для первого индивида:

MRS1^ (x, y) = [Уj .

Для второго индивида

dU2 = 1 1 y dU2 = 1 1 x

dx x x + y x(x + y) dy y x + y y(x + y) так что

MRSxy (x, y) = dU/dx = {yT. xyK У" dU2/ dy ^ x J

Таким образом, для любых комбинаций (x, y) предельные нормы замены для обоих индивидов совпадают, следовательно, совпадают и их предпочтения.

Концепция порядковой полезности служит основой теории потребительского выбора при отсутствии риска. Для теоретического описания потребительского поведения в рисковой ситуации она оказывается недостаточной. В теории выбора в условиях риска утверждается существование такой функции полезности, к максимизации математического ожидания которой стремится потребитель (функция полезности фон Неймана-Моргенштерна). В этом отношении предпочтения индивидов в данной задаче различны, если условиями заданы функции полезности фон Неймана-Моргенштерна. Допустим, что в рассматриваемых примерах цены продуктов численно равны, так что, как легко проверить, в выбираемых обоими потребителями наборах x = y. Допустим также, что потребителю предлагают указать набор благ, столь же полезный, как лотерея из наборов (1, 1) и (5, 5) с равными вероятностями. Так как x x/(x + x) = x/2, первый потребитель укажет набор (x, x), удовлетворяющий условию:

0.5 .1 + 0.5 . 5 = x,

откуда x = 3, так что он укажет набор (3, 3). Соответствующее условие для второго потребителя:

0.5 . ln1 + 0.5 . ln5 = lnx,

откуда x = \ PxPy" Py +4 PxPy

в) Последние равенства показьпвают, что при фиксированной величине дохода объем спроса на каждое благо снижается

как при росте цены этого, так и при росте цены другого блага.

Это означает, что блага являются взаимно дополняющими.

РЕШЕНИЕ ЗАДАЧИ № 8

а, б) Рассуждая по аналогии с решением предыдущей задачи, находим:

MRSxy =л \% = ^ =

Отсюда y = x (p /pY)2 = 4x. Из равенства дохода и расходов, 10x + 5 4x = 60, находим x = 2, y = 8.

Зависимость объемов спроса от цен и дохода описывается равенствами

px ■ (1 + px / py) py ■ (1 + py / px)

в) Последние равенства показывают, что при фиксированной величине дохода объем спроса на каждое благо сни

жается при росте цены этого блага, но возрастает с увеличением цены другого блага. Это означает, что блага являются взаимно заменяющими.

РЕШЕНИЕ ЗАДАЧИ № 9

Найдем выражения для предельных полезностей: dU = J__ dU_ = 1

Так как в точке потребительского оптимума предельная норма замены равна соотношению цен, справедливо равенство

откуда непосредственно находится объем потребления блага X: x = Е = Ё5 = 1.25

Спрос на благо X, как мы видим, не зависит от дохода (в дальнейшем нам придется уточнить это утверждение). Спрос на Y явным образом от дохода зависит. При I = 70 имеем:

70 -у/16 25 „

Ясно, что объем потребления не может быть отрицательным. Но, согласно полученному выражению для у, условие у > 0 выполняется при I > 4~РхРу = 20 и нарушается в противном случае. Естественно предположить, что при нарушении этого условия домашнее хозяйство полностью отказывается от блага Y, так что y = 0. Но в таком случае и выражение для x становится неверным: так как весь доход расходуется на благо X, объем его потребления равен x = I/PX.

Для проверки этого предположения выясним, какие значения принимает предельная норма замены на бюджетной границе, описываемой равенством pXx + pYy = I. Из условия y > 0 следует, что pXx < I и x < I /pX. Поэтому на бюджетной границе

MRSxy = x > Т2" 7^Равенство MRSxy = pX /pY = 16/25 = 0.625 есть условие внутреннего потребительского оптимума. При I = 70 предельная норма замены на бюджетной границе не меньше 162/702 ~ 0.052, и в некоторой точке (а именно x = 1.25, y = = 2) она равна 0.625. Это и есть найденный выше внутренний оптимум. При I = 15 на бюджетной границе MRSxy > > 162/152 ~ 1.138 и значения, равного 0.625, на бюджетной линии не существует. Это означает, что потребительский оптимум занимает граничное, или, как его чаще называют в экономике, угловое положение. Таким образом,

У = при / > ^рхРу;

МЕТОДИЧЕСКИЕ ПОЯСНЕНИЯ

Ниже приведены примеры решения типовых задач и упражнений

Тема 1. Система макроэкономических взаимосвязей

Задача 26 . На основании данных, приведенных в таблице, определите:

1) ВНП по доходам;

2) ВНП по расходам;

5) национальный доход.

Решение

1 Определяем ВНП по доходам. Он включает амортизацию, косвенные налоги на бизнес, заработную плату наемных работников, дивиденды, процент, доходы от индивидуальных вложений, арендную плату, нераспределенные прибыли, налоги на прибыль корпораций, арендную плату:

ВНП по доходам = 1 010 + 786 + 5 810 + 196 + 290 + 158 + 40 + 650 + 784 = 9 724 млн. долл.

2 Определяем ВНП по расходам:

ВНП по расходам = C + Ig + Xn + G,

где C – личные потребительские расходы;

Ig – валовые внутренние частные инвестиции;

G – государственные закупки товаров и услуг;

Xn – чистый экспорт.

ВНП по расходам = 6 452 + 1 530 – 186 + 1 928 = 9 724 млн. долл.

ВНП по расходам должен быть равен ВНП по доходам.

3 Определим ВВП:

ВВП = ВНП – Хn = 9 724 + 186 = 9 910 млн. долл.

4 Определим ЧНП:

ЧНП = ВВП – А = 9 910 – 1 010 = 8 900 млн. долл.

где А – амортизация.

5 Определим национальный доход:

НД = ЧНП – косвенные налоги на бизнес,

НД = 8 900 – 786 = 8 114 млн. долл.

Задача 27. ВНП равен 9 000 ден. ед., потребительские расходы – 5 200 ден. ед., государственные расходы – 1 900 ден. ед., а чистый экспорт – 180 ден. ед. Рассчитайте:

1) величину валовых инвестиций;

2) ЧНП, если сумма амортизации равна 850 ден. ед.;

Если в этом примере чистый экспорт выражается положительной величиной, может ли она быть отрицательной. В каком случае?

Решение

1 ВНП по рас = С + Ig + G + Xn ,

где С - потребительские расходы;

Ig - валовые инвестиции;

G - государственные расходы;

Xn - чистый экспорт.

Ig = ВНП – С – G – Xn,

Ig = 9000 – 5200 – 1900 – 180 = 1820;

2 ЧНП = ВНП – А,

ЧНП = 9000 – 850 = 8150.

3 Если импорт будет больше экспорта.

Тема 2. Потребление, сбережение, инвестиции

Задача 14. Экономика характеризуется следующими данными:

а) функция потребления С = Са + MPC· Y;

б) автономные инвестиции Ia единиц;

в) государственные закупки G единиц;

г) предельная ставка налогообложения t;

д) трансфертные платежи TR.

Существующие производственные мощности позволяют увеличить национальный доход в 1,25 раза. Как государство должно изменить свои закупки, чтобы обеспечить полное использование производственных мощностей при сбалансированности государственного бюджета? Каким может быть изменение трансфертных платежей?

Решение

Определим равновесный уровень доходов:

m =1/(1– mpc (1– t)) = 1/(1 – 0,55· (1 – 0,1)) = 1,98;

A = Ca + G + Ia +TR· mpc,

A = 50 + 100 + 400 + 200 · 0,55 = 660;

Y = 1,98 · 660 = 1 306,8.

Определим изменение равновесного объема производства:

Y2 = 1,25 · 1 306,8 = 1 633,5.

Определим, на сколько должны измениться государственные закупки:

DY = 1 633,5 – 1 306,8 = 326,7;

DG = 326,7/1,98 = 165.

Определим, на какую величину должны измениться трансфертные платежи:

DTR · mpc = 165;

DTR = 165/0,55 = 300.

Задача 16. Если функция сбережений описывается формулой S = –30+0,1Y, а автономные инвестиции составляют величину 125, то каков будет равновесный уровень национального дохода?

Решение

При равновесном уровне национального дохода величина автономных инвестиций равна сбережению.

Тогда I = S ,

125 = – 30 + 0,1 у,

Y равн = 1 550.

Ответ : равновесный уровень национального дохода 1 550.

Задача 17 . Функция потребления задана формулой С = 100 + 0,2 Y.

1) постройте график потребления;

2) постройте график сбережения;

3) определите равновесный объем национального дохода;

4) определите величину мультипликатора расходов при условии, что доход составляет 0; 200; 400; 600; 800.

Решение

Построим таблицу:

1 По данным таблицы строим график потребления:

Рассчитаем равновесный доход аналитически.

Приравняем Y = С, тогда Y = 100 + 0,2Y.

2 По данным таблицы строим график сбережения:

Предельная склонность к сбережению равна:

MPS = 1 – MPC = 1– 0,2 = 0,8.

Тогда величина мультипликатора μ равна:

Тема . Методы линейной алгебры в экономическом анализе.

Цель . Решение экономических задач с элементами моделирования, опирающиеся на базовую основу линейной алгебры.

1. Справочный материал.

Понятие матрицы часто используется в практической деятельности, например, данные о выпуске продукции нескольких видов в каждом квартале года или нормы затрат нескольких видов ресурсов на производство продукции нескольких типов и т.д. удобно записывать в виде матрицы.

Задача 1. В некоторой отрасли m заводов выпускают n видов продукции. Матрица задаёт объёмы продукции на каждом заводе в первом квартале, матрица - соответственно во втором; (а ij , в ij) - объёмы продукции j -го типа на i -м заводе в 1-м и 2-м кварталах соответственно:

а) объёмы продукции;

б) прирост объёмов производства во втором квартале по сравнению с первым по видам продукции и заводам;

в) стоимостное выражение выпущенной продукции за полгода (в долларах), если л - курс доллара по отношению к рублю.

Решение:

а) Объёмы продукции за полугодие определяются суммой матриц, т.е. С=А+В=, где с ij - объём продукции j-го типа, произведённый за полугодие i-м заводом.

б) Прирост во втором квартале по сравнению с первым определяется разностью матриц, т.е.

Д=В-А= . Отрицательные элементы показывают, что на данном заводе объём производства уменьшился, положительные - увеличился, нулевые - не изменился.

в) Произведение лC= л(А+В) даёт выражение стоимости объёмов производства за квартал в долларах по каждому заводу и каждому предприятию.

Задача 2. Предприятие производит n типов продукции, используя m видов ресурсов. Нормы затрат ресурса i-го товара на производство единицы продукции j-го типа заданы матрицей затрат. Пусть за определённый отрезок времени предприятие выпустило количество продукции каждого типа, записанное матрицей.

Определить S - матрицу полных затрат ресурсов каждого вида на производство всей продукции за данный период времени, если

, . Решение . Матрица полных затрат ресурсов S определяется как произведение матриц, т.е. S=AX.

Т.е за данный период времени будет израсходовано 930 ед. ресурса 1-го вида, 960 ед. ресурса 2-го вида, 450 ед. ресурса 3-го вида, 630 ед. ресурса 4-го вида.

Задача 3. Завод производит двигатели, которые могут либо сразу потребовать дополнительной регулировки (в 40% случаев), либо сразу могут быть использованы (в 60% случаев). Как показывают статистические исследования, те двигатели, которые изначально требовали регулировки, потребуют дополнительной регулировки через месяц в 65% случаев, а в 35% случаев через месяц будут работать хорошо. Те же двигатели, которые не требовали первоначальной регулировки, потребуют её через месяц в 20% случаев и продолжат хорошо работать в 80% случаев. Какова доля двигателей, которые будут работать хорошо или потребуют регулировки через 2 месяца после выпуска? Через 3 месяца?

Решение.

В момент после выпуска доля хороших двигателей составляет 0,6, а доля требующих регулировки - 0,4. Через месяц доля хороших составит: 0,6 . 0,8+0,4 . 0,35=0,62. Доля требующих регулировки: 0,6 . 0,2+0,4 . 0,65=0,38. введём строку состояния X t в момент t; X t =(x 1t ; x 2t), где x 1t - доля хороших двигателей, x 2t - доля двигателей, требующих регулировки в момент t.

Матрица перехода, где - доля двигателей, которые в настоящее время находятся в состоянии (1- «хороший», 2- «требует регулировки»), а через месяц - в состоянии.

Очевидно, что для матрицы перехода сумма элементов каждой строки равна 1, все элементы неотрицательны.

Очевидно, =(0,6 0,4), .

Тогда через месяц,

через 2 месяца; через 3 месяца.

Найдём матрицы;

Отметим, что если - матрица перехода, то - тоже матрица перехода при любом натуральном t. Теперь

Очевидно, .

Задача 3. Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн. усл. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго - на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: а) в минувшем году; б) в текущем году?

Решение.

Пусть и - прибыли первого и второго отделений в минувшем году. тогда условие задачи можно записать в виде системы: Решив систему, получим Следователь, а) прибыль в минувшем году первого отделения -4 млн. усл. ед., а второго - 8 млн. усл. ед.; б) прибыль в этом году первого отделения 1,7 . 4=6,8 млн. усл. ед., второго 1,4 . 8=11,2 млн. усл. ед.

2.1. Три завода выпускают четыре вида продукции. Необходимо: а) найти матрицу выпуска продукции за квартал, если заданы матрицы помесячных выпусков А 1, А 2 , А 3 ; б) найти матрицы приростов выпуска продукции за каждый месяц В 1 и В 2 и проанализировать результаты:

2.2. Предприятие производит мебель трёх видов и продаёт её в четырёх регионах. Матрица задаёт цену реализации единицы мебели i-го типа в j-м регионе. Определить выручку предприятия в каждом регионе, если реализация мебели за месяц задана матрицей.

2.3 . По условию задачи 2 определить:1) полные затраты ресурсов 3-х видов на производство месячной продукции, если заданы нормы затрат матрицей и объём выпуска каждого из двух типов продукции;

2) стоимость всех затраченных ресурсов, если задана стоимость единиц каждого ресурса.

2.4 . В ремонтную мастерскую поступают телефонные аппараты, 70 % которых требуют малого ремонта, 20 % - среднего ремонта, 10% - сложного ремонта. Статистически установлено, что 10% аппаратов прошедших малый ремонт, через год требуют малого ремонта, 60% - среднего, 30% -сложного ремонта. Из аппаратов, прошедших средний ремонт, 20% требуют через год малого ремонта, 50% - среднего, 30% - сложного ремонта. Из аппаратов, прошедших сложный ремонт, через год 60% требуют малого ремонта, 40% - среднего. Найти доли из отремонтированных в начале года аппаратов, которые будут требовать ремонта того или иного вида: через 1 год; 2 года;3 года.

Практическое занятие.

Тема . Методы математического анализа для построения моделей СЭП.

Цель . Решение экономических задач с элементами моделирования, в которых применяются методы математического анализа.

1. Справочный материал.

Функции находят широкое применение в экономической теории и практике. Спектр используемых в экономике функций весьма широк: от простейших линейных до функций, получаемых по определённому алгоритму с помощью рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени.

Наиболее часто используемые в экономике следующие функции:

1. Функция полезности (функция предпочтения) - зависимость результата, эффекта некоторого действия от уровня (интенсивности) этого действия.

2. Производственная функция - зависимость результата производственной деятельности от обусловивших его факторов.

3. Функция выпуска - зависимость объёма производства от наличия или потребления ресурсов.

4. Функция издержек - зависимость издержек производства от объёма продукции.

5. Функции спроса, потребления и предложения - зависимость объёма спроса, потребления или предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.).

Учитывая, что экономические явления и процессы обуславливаются действием различных факторов, для их исследований широко используются функции нескольких переменных. Среди этих функций выделяют мультипликативные функции, позволяющие представить зависимую переменную в виде произведения факторных переменных, обращающих его в нуль при отсутствии действия хотя бы одного фактора.

Используются также сепарабельные функции, которые дают возможность выделить влияние различных факторов переменных на зависимую переменную, и в частности, аддитивные функции, представляющие одну и ту же зависимую переменную как при суммарном, но раздельном воздействии нескольких факторов, так и при одновременном их воздействии.

Кроме геометрического и механического существует ещё и экономический смысл производной. Во-первых, производная объема произведенной продукции по времени есть производительность труда в момент. Во-вторых, существует ещё одно понятие, характеризующее экономический смысл производной. Если издержки производства y рассматривать как функцию количества выпускаемой продукции x, - прирост продукции, - приращение издержек производства, а - среднее приращение издержек производства на единицу продукции, тогда производная равная выражает предельные издержки производства и характеризует приближённо дополнительные затраты на производство единицы дополнительной продукции.

Предельные издержки зависят от уровня производства (количества выпускаемой продукции) x и определяются не постоянными производственными затратами, а лишь переменными (на сырьё, топливо ит.п.). Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность и др.предельные величины.

Предельные величины характеризуют не состояние, а процесс, то есть изменение экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Следует учесть, что экономика не всегда позволяет использовать предельные величины в силу неделимости многих объектов экономических расчётов и прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных ит.д.). Вместе с тем в ряде случаев можно отвлечься от дискретности показателей и эффективно предельные величины.

Для исследования экономических процессов и решения прикладных задач часто используется понятие эластичности функции.

Эластичностью функции называется предел отношения относительного приращения функции y к относительному приращению переменной x при:

Эластичность функции показывает приближённо, на сколько процентов изменится функция y=f(x) при изменении независимой переменной x на 1%. Это мера реагирования одной переменной величины на изменение другой.

Отметим свойства эластичности функции.

1. Эластичность функции равна произведению независимой переменной x на темп изменения функции, т.е. .

2. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций: , .

Эластичность функций применяется при анализе спроса и потребления. Например, эластичность спроса y относительно цены x - коэффициент, определяемый по формуле (1) и показывающий приближённо, на сколько процентов изменится спрос (объем потребления) при изменении цены (или дохода) на 1%.

Если эластичность спроса (по абсолютной величине) , то спрос считают эластичным, если - нейтральным, если - неэластичным относительно цены (или дохода).

В практической деятельности часто приходится сталкиваться с такими задачам, которые рационально решать методами математического анализа. Это задачи на нахождение объёма продукции при известном значении прибыли, определении уровня потребления товаров при известном доходе, определение момента времени рентабельности производства, определение размеров вклада при известных начальных вложениях и т.п.

Задача 1. Издержки y (в руб.) на изготовление партии деталей определяются по формуле, где - объём партии. Для первого варианта технологического процесса. Для второго варианта известно, что (руб.) при (дет.) и (руб.) при (дет.). Провести оценку двух вариантов технологического процесса и найти себестоимость продукции для обоих вариантов при (дет.)

Решение .

Для второго варианта определяем параметры и из системы уравнений:

откуда и, т.е. .

Точка (х 0 ,y 0) пересечения двух прямых находится из системы их уравнений:

откуда, .Очевидно, при объёме партии выгоднее второй вариант технологического процесса, при - первый вариант. Себестоимость продукции (руб.) при по первому варианту составляет, а по второму - .

Задача 2. Постоянные издержки составляют 125 тыс.руб. в месяц, а переменные издержки - 700 руб. за каждую единицу продукции. Цена единицы продукции 1200 руб. Найти объём продукции, при котором прибыль равна: а) нулю (точка безубыточности); б) 105 тыс.руб. в месяц.

Решение:

а) Издержки производства единиц продукции составят: (тыс.руб.). Совокупный доход (выручка) от реализации этой продукции, а прибыль (тыс.руб.). Точка безубыточности, в которой, равна (ед.).

б) Прибыль (тыс.руб.), т.е. при (ед.).

Задача 3. Продолжительность выполнения (мин.) при повторных операциях связана с числом этих операций зависимостью. Вычислить, сколько минут выполняется работа при 50 операциях, если известно, что при, а при.

Решение . Найдём параметры и, учитывая, что, . Получаем систему: решая которую найдём, .

Итак, при, (мин.)

Задача 4. Объём продукции u, произведённый бригадой рабочих, может быть описан уравнением (ед.), где t - рабочее время в часах. Вычислить производительность труда, скорость и темп её изменения через час после начала работы и за час до её окончания.

Решение. Производительность труда выражается производной (ед./час), а скорость и темп изменения производительности - соответственно производной и логарифмической производной: (ед./ч 2),

В заданные моменты времени и соответственно имеем: z(t)=112,5 (ед./ч), z"(t)=-20(ед./ч 2), T z (7)=-0,24 (ед./ч).

Итак, к концу работы производительность труда существенно снижается; при этом изменение знака z"(t) и T z (t) с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется её снижением в последние часы.

Задача 5. Опытным путём установлены функции спроса и предложения, где q и s - количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, p - цена товара.

Найти: а) равновесную цену, т.е.цену при которой спрос равен предложению;

б) эластичность спроса и предложения для этой цены;

в) изменение дохода при увеличении цены на 5% от равновесной.

Решение. а) Равновесная цена находится из условия q=s , тогда, откуда p= 2, т.е равновесная цена 2 ден.ед.

б) Найдём эластичность по спросу и предложению по формуле (1)

; . Для равновесной цены p=2 имеем; . Так как полученные значения эластичностей по абсолютной величине меньше 1, то и спрос и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это означает, что изменение цены не приведёт к резкому изменению спроса и предложения. Так, при увеличении цены p на 1% спрос уменьшится на 0,3%, а предложение увеличится на 0,8%.

в) При увеличении цены p на 5% от равновесной спрос уменьшится на 5 . 0,3=1,5%, следовательно, доход возрастёт на 3,5%.

Задача 6. Зависимость между издержками производства y и объёмом выпускаемой продукции x выражается функцией (ден.ед.). Определить средние и предельные издержки при объёме продукции 10 ед.

Решение. Функция средних издержек выражается соотношением; при x= 10 средние издержки (на единицу продукции) равны (ден. ед.). Функция предельных издержек выражается производной; при x= 10 предельные издержки составят (ден.ед.). Итак, если средние издержки на производство единицы продукции составляют 45 ден.ед., то предельные издержки, т.е. дополнительные затраты на производство дополнительной единицы продукции при данном уровне производства (объёме выпускаемой продукции 10 ед.) , составляют 35 ден.ед.

Задача 7. Выяснить, чему равны предельные и средние полные затраты предприятия, если эластичность полных затрат равна 1?

Решение . Пусть полные затраты предприятия y выражаются функцией, где x - объём выпускаемой продукции. Тогда средние затраты y 1 на производство единицы продукции. Эластичность частного двух функции равна разности их эластичностей, т.е. .

По условию, следовательно, . Это означает, что с изменением объёма продукции средние затраты на единицу продукции не меняются, т.е., откуда.

предельные издержки предприятия определяются производной. Итак, т.е предельные издержки равны средним издержкам(полученное утверждение справедливо только для линейных функций издержек).

2. Задания для самостоятельной работы.

2.1. Издержки перевозки двумя видами транспорта выражаются уравнениями: и, где - расстояния в сотнях километров, - транспортные расходы. Начиная с какого расстояния более экономичен второй вид транспорта?

2.2. Зная, что изменение объёма производства с изменением производительности труда происходит по прямой линии, составить её уравнение, если при =3 =185, а при =5 =305. Определить объём производства при =20.

2.3 . Предприятие купило автомобиль стоимостью 150 тыс.руб. Ежегодная норма амортизации составляет 9%. Полагая зависимость стоимости автомобиля от времени линейной, найти стоимость автомобиля через 4,5 года.

2.4. Зависимость уровня потребления некоторого вида товаров от уровня дохода семьи выражается формулой: . Найти уровень потребления товаров при уровне дохода семьи 158 ден.ед. Известно, что при =50 =0; =74 =0,8; =326 =2,3.

2.5. Банк выплачивает ежегодно 5% годовых (сложный процент). Определить: а) размер вклада через 3 года, если первоначальный вклад составил 10 тыс. руб.; б) размер первоначального вклада, при котором через 4 года вклад (вместе с процентными деньгами) составит 10 000 руб.

Указание. Размер вклада через t лет определяется по формуле, где p-процентная ставка за год, Q 0 -первоначальный вклад.

2.6. Затраты на производство продукции (тыс.руб.) выражаются уравнением, где -количество месяцев. Доход от реализации продукции выражается уравнением. Начиная с какого месяца производство будет рентабельным?

2.7. Зависимость между себестоимостью единицы продукции y (тыс. руб.) и выпуском продукции x (млрд.руб.) выражается функцией. Найти эластичность себестоимости при выпуске продукции, равном 60 млрд.руб.

Практическое занятие.

Тема. Предельный анализ экономических процессов.

Цель. Рассмотреть применение математических методов для нахождения предельных величин в оптимизационных задачах.

1. Справочный материал.

Функция издержек С(х) определяет затраты, необходимые для производства x единиц данного продукта. Прибыль, где D(x) - доход от производства x единиц продукта.

Средние издержки A(x) при производстве x единиц продукта есть.Предельные издержки.

Оптимальным значением выпуска для производителя является то значение x единиц продукта, при котором прибыль P(x) оказывается наибольшей.

Задача 1. Функция издержек имеет вид. На начальном этапе фирма организует производство так, чтобы минимизировать средние издержки A(x) . В дальнейшем на товар устанавливается цена, равная 4 усл.ед. за единицу. На сколько единиц товара фирме следует увеличить выпуск?

Решение. Средние издержки принимают минимальное значение при x =10. Предельные издержки. При установившейся цене оптимальное значение P(x) выпуска задаётся условием максимизации прибыли: , т.е. 4=M(x) , откуда. Таким образом, производство следует увеличить на 10 единиц.

Задача 2. Определить оптимальное для производителя значение выпуска x 0 , при условии, что весь товар реализуется по фиксированной цене за единицу p =14 , если известен вид функции издержек.

Решение . По формуле прибыли получаем, .

Находим производную прибыли по объёму: , тогда х опт = 2.

Задача 3. Найти максимальную прибыль, которую может получить фирма производитель, при условии, что весь товар реализуется по фиксированной цене за единицу р =10,5 и функция издержек имеет вид.

Решение . Находим значение прибыли.

Производная прибыли по объёму имеет вид: . Тогда, . .

2. Задания для самостоятельной работы.

2.1 Определить оптимальное для производителя значение выпуска x0, при условии, что весь товар реализуется по фиксированной цене за единицу p=8 и известен вид функции издержек.

2.2 Найти максимальную прибыль, которую может получить фирма-производитель, при условии, что весь товар реализуется по фиксированной цене за единицу p =40 и известен вид функции издержек.

2.3 При производстве монополией x единиц товара за единицу. Определить оптимальное для монополии значение выпуска x 0 (предполагается что весь произведённый товар реализуется), если издержки имеют вид.

2.4 Функция издержек имеет вид. Доход от реализации единицы продукции равен 50. Найти максимальное значение прибыли, которое может получить производитель.

2.5 На начальном этапе производства фирма минимизирует средние издержки, причём функция издержек имеет вид. В дальнейшем цена на единицу товара устанавливается равной р =37. На сколько единиц товара фирме следует увеличить выпуск? На сколько при этом изменятся средние издержки?

Задания для контрольной работы.

ПОТРЕБЛЕНИЕ И СПРОС

2.1 Задачи

Задача № 1

Объем потребления некоторого товара домашним хозяйством

(q) в зависимости от дохода (I) описывается равенством:

Определить, при каких значениях дохода товар для

данного домашнего хозяйства является

а) низшим благом;

б) нормальным благом;

в) необходимым благом;

г) роскошным благом.

Задача № 2 Индивид потребляет два блага в количествах x и y соответственно. Согласуются ли приведенные ниже функции полезности с аксиомами потребительских предпочтений? (да/нет)

а) U(x, y) = x2 + y 2 ;

в) U(x, y) = +.

xy Задача № 3 Предпочтения индивида характеризуются предельными нормами замещения MRSxy = 2, MRSxz = 0.8. Найти предельные нормы замещения а) MRSyx, б) MRSzx, в) MRSyz, г) MRSzy.

16 Часть II.

Задача № 4 Домашнее хозяйство потребляет два блага в количествах x и y; его предпочтения описываются функцией полезности U(x, y). Найти функцию спроса домашнего хозяйства, если

а) U(x, y) = x3y2;

б) U(x, y) = xy.

Задача № 5 Предпочтения двух индивидов описываются функциями полезности xy U1 (x, y) = U2 (x, y) = ln x + ln y ln(x + y).

x+y Различаются ли предпочтения этих индивидов?

Задача № 6 Рассмотрим модель, в которой предпочтения потребителя относятся не к продуктам, а к характеристикам, которыми продукты обладают (модель Ланкастера). Допустим, что рассматривается множество продуктов, обладающих двумя характеристиками (X и Y).

Обозначим (xi, yi) количественные меры соответствующих характеристик в единице i-го продукта, причем простоты ради в качестве единицы каждого продукта принимается количество продукта, приобретаемое за одну денежную единицу. Будем считать, что предпочтения в пространстве Потребление и спрос. 17 характеристик удовлетворяют тем же аксиомам, что и предпочтения в пространстве благ в традиционной теории.

Задача № 7 Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его доход I = 60, а предпочтения опиxy сываются функцией полезности U(x, y) =.

а) Найти объемы спроса на каждое из благ при ценах благ pX = 9, pY = 4.

Задача № 8 Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его предпочтения описываются функцией полезности U(x, y) = x + y. Известен доход: I = 60.

а) Найти объемы спроса на каждое из благ при ценах благ pX = 10, pY = 5.

б) Определить зависимости объемов спроса на каждое из благ от цен и дохода.

в) Определить характер взаимозависимости благ в потреблении.

Задача № 9

– – –

б) Определить зависимости от дохода объемов спроса на каждое из благ.

Задача № 10 Индивид потребляет два блага, X и Y, в количествах x и y соответственно.

Функция полезности индивида:

U = ax + by + xy, a 0, b 0.

а) Пусть a = 10, b = 25. Определить объемы потребления благ, если цены благ pX = 5, pY = 2 при доходе индивида I = 200;

б) то же при доходе индивида I = 100;

в) при каких соотношениях дохода и цен оптимум потребителя будет внутренним (x 0, y 0)?

Задача № 11

Домашнее хозяйство приобретает благо X, производимое естественной монополией, по цене pX = 10 в количестве x = = 5. Государство, регулирующее цену продукта естественной монополии, сочло целесообразным повысить цену до pX = = 14 и выплачивать домашнему хозяйству компенсацию в размере (pX – pX) x = 20.

а) Изменилось ли благосостояние домашнего хозяйства, и если да, то в какую сторону?

б) Проверить утверждение на следующем примере: домашнее хозяйство кроме блага X потребляет еще одно благо, Y, цена которого pY = 1 не изменилась; доход домашнего хозяйства I = 100, а функция полезности U(x, y) = xy.

Задача № 12 Классификация благ, основанная на кривых Энгеля, учитывает изменения доли дохода, направленной на покупку рассматриваемого блага, в зависимости от изменения дохода.

Докажите следующие утверждения:

Потребление и спрос. 19 если доля дохода, направляемая на покупку данного блага, увеличивается с ростом дохода, то эластичность объема потребления по доходу больше единицы;

Задача № 13

Домашнее хозяйство потребляет три блага, X, Y и Z. Их доли в расходах составляют соответственно sX = 50%, sY = = 30%, sZ = 20%. Известны эластичности по доходу объемов потребления благ X и Y: EI[x] = 2, EI[y] = 0.6.

а) Найти эластичность объема потребления блага Z по доходу.

б) Определить, к какому типу относится каждое из благ.

Задача № 14 Докажите утверждение: если среди благ, потребляемых домашним хозяйством, есть хотя бы одно низшее, то среди них имеется также хотя бы одно роскошное.

Задача № 15 Телефонная компания предлагает потребителям услуг на выбор два варианта тарифов: (а) 4 ед./мин без абонентской платы; (б) 2 ед./мин и абонентская плата 20 ед.

Какой из тарифов выберет каждый из следующих потребителей:

1) функция полезности U1 = x0.5y0.5, доход I1 = 100 ед.;

2) функция полезности U2 = x0.25y0.75, доход I2 = 100 ед.;

3) функция полезности U3 = x0.25y0.75, доход I3 = 200 ед.

Здесь x - количество (в минутах) потребляемых услуг телефонной компании, y - объем потребления всех других благ, цена которых равна 1 ед.

20 Часть II.

2.2 Решения Решение Задачи № 1 Из графика видно, что с ростом дохода от нуля до некоторого уровня объем потребления товара возрастает, так что благо является нормальным; при дальнейшем росте дохода данный товар вытесняется некоторым заменителем, объем его потребления снижается и товар становится низшим.

– – –

Комментарии.

1. Знак производной всегда совпадает со знаком эластичности. Поэтому ответы на все вопросы задачи можно было получить, рассматривая диапазоны уровней дохода, в пределах которых значения EI[q] превышают единицу, лежат между нулем и единицей и оказываются отрицательными.

2. Современная классификация потребляемых благ берет начало с исследований Э. Энгеля, выполненных в середине XIX в. и, естественно, не использовавших понятия эластичности функций. Проанализировав структуру потребительских бюджетов, Энгель установил, что с ростом дохода сумма расходов на питание возрастает, но их доля в распределении дохода падает. Если мы рассматриваем определенный товар, потребляемый в количестве q и покупаемый по цене p (которую мы считаем здесь неизменной), то расходы равны pq.

Доля, приходящаяся на данный товар, равна pq/I; если она с ростом дохода убывает, то EI 0. Воспользовавшись свойствами эластичности (см. Приложение) и учитывая неизменность цены, представим это соотношение в виде EI[q] – 1 0, или EI[q] 1. При этом абсолютная сумма расходов возрастает, EI = EI[q] 0. Таким образом, закон Энгеля применительно к необходимому благу (подобно продуктам питания) формулируется в виде двойного неравенства 0 EI[q] 1.

22 Часть II.

– – –

Доли расходов на каждое благо зависели не от абсолютных значений параметров и, а лишь от их соотношения.

Так, решение в п. а) не изменилось бы, если бы показатели степени равнялись не 3 и 2, а, скажем, 15 и 10 или 0.3 и

0.2. Последнее обстоятельство связано с тем, что функции полезности, связанные монотонно возрастающим преобразованием, представляют одну и ту же систему предпочтений (порядковая концепция полезности). Пусть x - вектор, представляющий набор благ, U1(x) и U2(x) - функции полезности, причем U2(x) = (U1(x)), где - монотонно возрастающая функция. В этом случае если U1(x1) U1(x2), то и U2(x1) U2(x2), т. е. набор, оцениваемый функцией U1 как более предпочтительный, так же оценивается и функцией U2. Возведение в положительную степень - монотонно возрастающее преобразование, и функция x15y10 = (x3y2)5 описывает ту же систему предпочтений, что и функция в задании a). Тот же результат дает и, например, логарифмирование:

U3(x) = 3 ln x + 2 ln y = ln(x3y2).

В заданиях потребитель ограничивался двумя благами, но выводы остаются справедливыми при произвольном числе благ. Пусть x = (x1, x2, …, xn) и n U (x) = xii, (1) i =1

– – –

Решение Задачи № 5 Нетрудно заметить, что U1(x, y) = ln U2(x, y). Логарифм - возрастающая функция. Если первый потребитель предпочитает набор (x1, y1) набору (x2, y2), т. е. если U1(x1, y1) U1(x2, y2), то U2(x1, y1) U2(x2, y2), а это означает, что второй потребитель также предпочитает первый набор второму. В рамках порядковой теории полезности предпочтения потребителей неразличимы.

Потребление и спрос. 27

– – –

Решение Задачи № 6 Одна из аксиом потребительских предпочтений - аксиома ненасыщаемости («больше лучше, чем меньше»). Поэтому представляется очевидным, что любой потребитель предпочтет продукт 2 продукту 1 (x2 x1 и y2 y1) - продукт 2 доминирует над продуктом 1. На рисунке область доминирования по отношению к продукту 1 («северо-восточный угол») показана штриховыми линиями; точка, соответствующая продукту 2, располагается в этой области. Если по отношению к данному продукту есть доминирующий (на графике он располагался бы правее и выше данного), то ни один потребитель не выберет данный продукт. Таким образом, продукт 1 не может быть продан.

Кроме того, продукт не может быть продан, если он уступает по обеим характеристикам некоторому набору продуктов, приобретаемому за ту же цену. Если в набор входят n продуктов в количествах i, таких что n

– – –

и если каждый из продуктов мог быть куплен за одну денежную единицу, то и набор может быть куплен также за одну единицу. Если некоторый продукт доминируется набором из других продуктов, то каждый потребитель предпочтет ему этот набор.

Если выбор осуществляется в пространстве двух характеристик, достаточно ограничиться двухпродуктовыми наборами; все возможные наборы из двух конкретных продуктов графически представляются отрезками, соединяющими точки, обозначающие эти продукты. Таким образом, если на графике правее и выше данного продукта имеются точки отрезка, соединяющего два других продукта, то это означает, что существуют наборы, доминирующие над данным продуктом. Если составить набор из третьего и пятого продуктов в количествах 3 =, 5 =, то мы получим набор с характеристиками x = 6 = x4 и y = 6 y4 (точка 4 на рисунке), доминирующий по отношению к четвертому продукту (для доминирования i над j требуется xi xj и yi yj, причем по крайней мере одно из неравенств должно быть строгим).

30 Часть II.

Решение Задачи № 7

– – –

Решение Задачи № 9

– – –

нарушении этого условия домашнее хозяйство полностью отказывается от блага Y, так что y = 0. Но в таком случае и выражение для x становится неверным: так как весь доход расходуется на благо X, объем его потребления равен x = I/pX.

Для проверки этого предположения выясним, какие значения принимает предельная норма замены на бюджетной границе, описываемой равенством pXx + pYy = I. Из условия y 0 следует, что pXx I и x I /pX. Поэтому на бюджетной границе p2 162 MRS XY = 2 X = 2.

I2 x I Равенство MRSXY = pX /pY = 16/25 = 0.625 есть условие внутреннего потребительского оптимума. При I = 70 предельная норма замены на бюджетной границе не меньше 162/702 0.052, и в некоторой точке (а именно x = 1.25, y = = 2) она равна 0.625. Это и есть найденный выше внутренний оптимум. При I = 15 на бюджетной границе MRSXY 162/152 1.138 и значения, равного 0.625, на бюджетной линии не существует. Это означает, что потребительский оптимум занимает граничное, или, как его чаще называют в экономике, угловое положение. Таким образом, Комментарий.

Если при некоторых значениях (x, y), лежащих на бюджетной границе, имеет место неравенство MRSXY pX /pY, то в интересах потребителя несколько увеличить потребление блага X, соответственно сократив потребление блага Y. Если неравенство имеет противоположный знак, то потребитель может повысить полезность потребляемого набора, сместившись вдоль бюджетной границы в сторону уменьшения Потребление и спрос. 33 потребления блага X и увеличения потребления блага Y.

Если в некоторой внутренней точке бюджетной границы выполняется равенство MRSXY = pX / pY, то, как следует из выпуклости кривых безразличия к началу координат, и увеличение, и уменьшение значения x привели бы к снижению полезности. Это и означает, что в данной точке достигается потребительский оптимум. Но если на бюджетной границе всюду имеет место соотношение MRSXY pX/pY, то в каждой внутренней точке границы потребитель заинтересован в увеличении x, так что оптимум достигается при полном расходовании дохода на покупку блага X и отказе от блага Y.

Решение Задачи №10

– – –

объем потребления невозможен, полученный результат означает, что внутренний оптимум потребителя при данных условиях не существует. Следовательно, оптимум принимает граничное положение: x = 0, y = I/pY = 50. См. комментарий к предыдущей задаче.

Решение Задачи № 11

– – –

от дохода рассматривается в предположении фиксированных цен, для эластичности доли справедливо равенство EI[s] = EI = EI[x] – 1 (см. Приложение). Для возрастающей доли EI[s] 0, для убывающей доли EI[s] 0, откуда следуют оба утверждения.

Студент приобретает кофе и пирожки. Цена чашки кофе $2, пирожка $3. При этом он располагает бюджетом в размере $23. Известны предпочтения студента в виде общей полезности:

Как потратить максимум бюджета так, чтобы купить набор этих двух благ с наибольшей полезностью? Сколько она составит?

Решение:

Оптимальный объём потребления достигается при выполнении второго закона Госсена - закона равной маржинальной (предельной) полезности на единицу затрат: отношение предельной полезности блага к его цене должно быть одинаковым для всех благ.

Запишем этот закон в виде тождества:

MU к - предельная полезность кофе,

MU п - предельная полезность пирожков,

P к - цена кофе,

P п - цена пирожков.

Перепишем это равенство в более удобном виде:

Значит, цены на кофе и пирожки относятся как 2:3. Теперь надо найти такую комбинацию предельных полезностей, чтобы они относились также как 2:3.

Рассчёт предельной полезности произведём по формуле:

ΔTU - приращение общей полезности (TU 1 - TU 0) ,

ΔQ - приращение количества (Q 1 - Q 0) .

Так как количество в нашей задаче прирастает каждый раз на единицу ΔQ = 1 , можно упростить эту формулу так:

MU = ΔTU

Количество	1	2	3	4	5	6	7
TU кофе, ютилей	20	36	50	62	72	80	86
MU кофе, ютилей	20	16	14	12	10	8	6
TU пирожков, ютилей	36	66	93	117	135	144	150
MU пирожков, ютилей	36	30	27	24	18	9	6