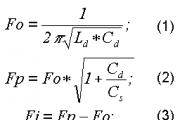Расчеты структурной надежности систем. Показатели, характеризующие безотказность Расчет основных показателей надежности
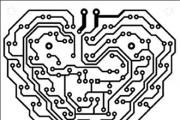
Структурная схема надежности приведена на рис 7.1. Значения интенсивности отказов элементов даны в 1/ч.

1. В исходной схеме
элементы 2 и 3 образуют параллельное
соединение. Заменяем их квазиэлементом
А. Учитывая, что  , получим
, получим
2. Элементы 4 и 5
также образуют параллельное соединение,
заменив которое элементом В и учитывая,
что , получим
, получим
3. Элементы 6 и 7 в
исходной схеме соединены последовательно.
Заменяем их элементом С, для которого
при
 . (7.3)
. (7.3)
4. Элементы 8 и 9
образуют параллельное соединение.
Заменяем их элементом D, для которого
при  ,
получим
,
получим
5. Элементы 10 и 11 с
параллельным соединением заменяем
элементом Е, причем, так как  ,
то
,
то
6. Элементы 12 , 13 , 14 и 15 образуют соединение “2 из 4”, которое заменяем элементом F. Так как, то для определения вероятности безотказной работы элемента F можно воспользоваться комбинаторным методом (см. раздел 3.3):
 (7.6)
(7.6)

7. Преобразованная схема изображена на рис. 7.2.
8. Элементы A, B, C, D и Е образуют (рис. 7.2) мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента (см. раздел 3.4), в качестве которого выберем элемент С. Тогда
где  - вероятность безотказной работы
мостиковой схемы при абсолютно надежном
элементе С (рис. 7.3, а),
- вероятность безотказной работы
мостиковой схемы при абсолютно надежном
элементе С (рис. 7.3, а),  - вероятность безотказной работы
мостиковой схемы при отказавшем элементе
С (рис. 7.3, б).
- вероятность безотказной работы
мостиковой схемы при отказавшем элементе
С (рис. 7.3, б).

Учитывая, что  ,
получим
,
получим
 (7.8)
(7.8)
9. После преобразований схема изображена на рис. 7.4.

 (7.9)
(7.9)
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 7.1) подчиняются экспоненциальному закону:
 (7.10)
(7.10)
12. Результаты
расчетов вероятностей безотказной
работы элементов 1 - 15 исходной схемы
по формуле (7.10) для наработки до  часов представлены в таблице 7.1.
часов представлены в таблице 7.1.
13. Результаты расчетов вероятностей безотказной работы квазиэлементов A, B, C, D, E, F и G по формулам (7.1) - (7.6) и (7.8) также представлены в таблице 7.1.
14. На рис. 7.5 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.
15. По графику (рис.
7.5, кривая P) находим для 

 - процентную наработку системы
- процентную наработку системы  ч.
ч.
16. Проверочный
расчет при  ч показывает (таблица 7.1), что
ч показывает (таблица 7.1), что  .
.
17. По условиям
задания повышенная  - процентная наработка системы
ч.
- процентная наработка системы
ч.
Таблица 7.1
Расчет вероятности безотказной работы системы
|
Наработка t, x 10 6 ч |
|||||||||

Рис 7.5. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`) и системы со структурным резервированием элементов (Р``).
18. Расчет показывает
(таблица 7.1), что при  ч для элементов преобразованной схемы
(рис. 7.4)
ч для элементов преобразованной схемы
(рис. 7.4)  ,
,
 и
и  .
Следовательно, из трех последовательно
соединенных элементов минимальное
значение вероятности безотказной работы
имеет элемент F (система “2 из 4” в
исходной схеме (рис. 7.1)) и именно увеличение
его надежности даст максимальное
увеличение надежности системы в целом.
.
Следовательно, из трех последовательно
соединенных элементов минимальное
значение вероятности безотказной работы
имеет элемент F (система “2 из 4” в
исходной схеме (рис. 7.1)) и именно увеличение
его надежности даст максимальное
увеличение надежности системы в целом.
19. Для того, чтобы
при  ч система в целом имела вероятность
безотказной работы
ч система в целом имела вероятность
безотказной работы  ,
необходимо, чтобы элемент F имел
вероятность безотказной работы (см.
формулу (7.9))
,
необходимо, чтобы элемент F имел
вероятность безотказной работы (см.
формулу (7.9))
 (7.11)
(7.11)
При этом значении элемент F останется самым ненадежным в схеме (рис. 7.4) и рассуждения в п.18 останутся верными.
Очевидно, значение
 ,
полученное по формуле (7.11), является
мини-мальным для выполнения условия
увеличения наработки не менее, чем в
1.5раза,
при более высоких значениях
,
полученное по формуле (7.11), является
мини-мальным для выполнения условия
увеличения наработки не менее, чем в
1.5раза,
при более высоких значениях  увеличение надежности системы будет
большим.
увеличение надежности системы будет
большим.
20. Для определения
минимально необходимой вероятности
безотказной работы элементов 12 - 15 (рис.
7.1) необходимо решить уравнение (7.6)
относительно  при
при  .
Однако, т.к. аналитическое выражение
этого уравнения связано с определенными
трудностями, более целесообразно
использовать графо-аналитический метод.
Для этого по данным табл. 7.1 строим график
зависимости
.
Однако, т.к. аналитическое выражение
этого уравнения связано с определенными
трудностями, более целесообразно
использовать графо-аналитический метод.
Для этого по данным табл. 7.1 строим график
зависимости  .
График представлен на рис. 7.6.
.
График представлен на рис. 7.6.

Рис. 7.6. Зависимость вероятности безотказной работы системы “2 из 4” от вероятности безотказной работы ее элементов.
21. По графику при
 находим
находим  .
.
22. Так как по
условиям задания все элементы работают
в периоде нормальной эксплуатации и
подчиняются экспоненциальному закону
(7.10), то для элементов 12 - 15 при  находим
находим
ч . (7.12)
. (7.12)
23. Таким образом,
для увеличения  - процентной наработки системы необходимо
увеличить надежность элементов 12, 13, 14
и 15 и снизить интенсивность их отказов
с
- процентной наработки системы необходимо
увеличить надежность элементов 12, 13, 14
и 15 и снизить интенсивность их отказов
с  до
до  ч
ч ,
т.е. в 1.55 раза.
,
т.е. в 1.55 раза.
24. Результаты
расчетов для системы с увеличенной
надежностью элементов 12, 13, 14 и 15 приведены
в таблице 7.1. Там же приведены расчетные
значения вероятности безотказной работы
системы “2 из 4” F` и системы в целом P`.
При  ч
вероятность безотказной работы системы
,
что соответствует условиям задания.
График приведен на рис 7.5.
ч
вероятность безотказной работы системы
,
что соответствует условиям задания.
График приведен на рис 7.5.
25. Для второго
способа увеличения вероятности
безотказной работы системы - структурного
резервирования - по тем же соображениям
(см. п. 18) также выбираем элемент F,
вероятность безотказной работы которого
после резервирования должна быть не
ниже  (см. формулу (7.11)).
(см. формулу (7.11)).
26. Для элемента F
- системы “2 из 4” - резервирование
означает увеличение общего числа
элементов. Аналитически определить
минимально необходимое количество
элементов невозможно, т.к. число элементов
должно быть целым и функция  дискретна.
дискретна.
27. Для повышения надежности системы “2 из 4” добавляем к ней элементы, идентичные по надежности исходным элементам 12 - 15, до тех пор, пока вероятность безотказной работы квазиэлемента F не достигнет заданного значения.
Для расчета воспользуемся комбинаторным методом (см. раздел 3.3) :
Добавляем элемент 16, получаем систему “2 из 5”:
 (7.13)
(7.13)
- добавляем элемент 17, получаем систему “2 из 6”:
 (7.15)
(7.15)
Добавляем элемент 18, получаем систему “2 из 7”:
 (7.17)
(7.17)

28. Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис. 7.1) систему “2 из 4” достроить элементами 16, 17 и 18 до системы “2 из 7” (рис. 7.7).
29. Результаты расчетов вероятностей безотказной работы системы “2 из 7” F`` и системы в целом P`` представлены в таблице 7.1.
30. Расчеты
показывают, что при  ч
,
что соот-ветствует условию задания.
ч
,
что соот-ветствует условию задания.
31. На рис. 7.5 нанесены
кривые зависимостей вероятности
безотказной работы системы после
повышения надежности элементов 12 - 15
(кривая  )
и после структурного резервирования
(кривая
)
и после структурного резервирования
(кривая  ).
).
1. На рис. 7.5
представлена зависимость вероятности
безотказной работы системы (кривая  ).
Из графика видно, что 50% - наработка
исходной системы составляет
).
Из графика видно, что 50% - наработка
исходной системы составляет  часов.
часов.
2. Для повышения
надежности и увеличения 50% - наработки
системы в 1.5 раза (до  часов)
предложены два способа:
часов)
предложены два способа:
а) повышение
надежности элементов 12, 13, 14 и 15 и
уменьшение их отказов с  до
до  ч
ч ;
;
б) нагруженное резервирование основных элементов 12, 13, 14 и 15 идентичными по надежности резервными элементами 16, 17 и 18 (рис. 7.7).
3. Анализ зависимостей
вероятности безотказной работы системы
от времени (наработки) (рис. 7.5) показывает,
что второй способ повышения надежности
системы (структурное резервирование)
предпочтительнее первого, так как в
период наработки до  часов вероятность безотказной работы
системы при структурном резервировании
(кривая
часов вероятность безотказной работы
системы при структурном резервировании
(кривая  )
выше, чем при увеличении надежности
элементов (кривая
)
выше, чем при увеличении надежности
элементов (кривая  ).
).
ПРИЛОЖЕНИЕ
Биномиальные
коэффициенты

Введение
1. Количественные характеристики безотказности
2. Структурно - логический анализ технических систем
3. Расчеты структурной надежности систем
3.1. Системы с последовательным соединением элементов
3.2. Системы с параллельным соединением элементов
3.3. Системы типа “m из n “
3.4. Мостиковые системы
3.5. Комбинированные системы
4. Повышение надежности технических систем
4.2. Расчет надежности систем c резервированием
6. Исходные данные к работе
7. Пример расчета надежности
Приложение
Литература
ВВЕДЕНИЕ
Надежностью называют свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки. Расширение условий эксплуатации, повышение ответственности выполняемых радиоэлектронными средствами (РЭС) функций, их усложнение приводит к повышению требований к надежности изделий.
Надежность является сложным свойством, и формируется такими составляющими, как безотказность, долговечность, восстанавливаемость и сохраняемость. Основным здесь является свойство безотказности - способность изделия непрерывно сохранять работоспособное состояние в течение времени. Потому наиболее важным в обеспечении надежности РЭС является повышение их безотказности.
Особенностью проблемы надежности является ее связь со всеми этапами “жизненного цикла” РЭС от зарождения идеи создания до списания: при расчете и проектировании изделия его надежность закладывается в проект, при изготовлении надежность обеспечивается, при эксплуатации - реализуется. Поэтому проблема надежности - комплексная проблема и решать ее необходимо на всех этапах и разными средствами. На этапе проектирования изделия определяется его структура, производится выбор или разработка элементной базы, поэтому здесь имеются наибольшие возможности обеспечения требуемого уровня надежности РЭС. Основным методом решения этой задачи являются расчеты надежности (в первую очередь - безотказности), в зависимости от структуры объекта и характеристик его составляющих частей, с последующей необходимой коррекцией проекта. Некоторые способы расчета структурной надежности рассматриваются в данном пособии.
1. КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ БЕЗОТКАЗНОСТИ
Безотказность (и другие составляющие свойства надежности) РЭС проявляется через случайные величины: наработку до очередного отказа и количество отказов за заданное время. Поэтому количественными характеристиками свойства здесь выступают вероятностные переменные.
Наработка есть продолжительность или объем работы объекта. Для РЭС естественно исчисление наработки в единицах времени, тогда как для других технических средств могут быть удобнее иные средства измерения (например, наработка автомобиля - в километрах пробега). Для невосстанавливаемых и восстанавливаемых изделий понятие наработки различается: в первом случае подразумевается наработка до первого отказа (он же является и последним отказом), во втором - между двумя соседними во времени отказами (после каждого отказа производится восстановление работоспособного состояния). Математическое ожидание случайной наработки Т
(1.1)является характеристикой безотказности и называется средней наработкой на отказ (между отказами). В (1.1) через t обозначено текущее значение наработки, а f(t ) - плотность вероятности ее распределения.
Вероятность безотказной работы - вероятность того, что в пределах заданной наработки t отказ объекта не возникнет:
(1.2)Вероятность противоположного события называется вероятностью отказа и дополняет вероятность безотказной работы до единицы:
(1.3)В (1.2) и (1.3) F(t ) есть интегральная функция распределение случайной наработки t . Плотность вероятности f(t ) также является показателем надежности, называемым частотой отказов :
(1.4)Из (1.4) очевидно, что она характеризует скорость уменьшения вероятности безотказной работы во времени.
Интенсивностью отказов называют условную плотность вероятности возникновения отказа изделия при условии, что к моменту t отказ не возник:
Функции f(t) и
(t) измеряются в ч.Интегрируя (1.5), легко получить:
(1.6)Это выражение, называемое основным законом надежности, позволяет установить временное изменение вероятности безотказной работы при любом характере изменения интенсивности отказов во времени. В частном случае постоянства интенсивности отказов
(t ) == const (1.6) переходит в известное в теории вероятностей экспоненциальное распределение:Поток отказов при
(t )=const называется простейшим и именно он реализуется для большинства РЭС в течении периода нормальной эксплуатации от окончания приработки до начала старения и износа.Подставив выражение плотности вероятности f(t ) экспоненциального распределения (1.7) в (1.1), получим:
(1.8)т.е. при простейшем потоке отказов средняя наработка Т 0 обратна интен-сивности отказов
. С помощью (1.7) можно показать, что за время средней наработки, t=T 0 , вероятность безотказной работы изделия составляет 1/е. Часто используют характеристику, называемую - процентной наработкой - время, в течении которого отказ не наступит с вероятностью (%): (1.9)Выбор параметра для количественной оценки надежности определяется назначением, режимами работы изделия, удобством применения в расчетах на стадии проектирования.
2. СТРУКТУРНО - ЛОГИЧЕСКИЙ АНАЛИЗ ТЕХНИЧЕСКИХ СИСТЕМ
Конечной целью расчета надежности технических устройств является оптимизация конструктивных решений и параметров, режимов эксплуатации, организация технического обслуживания и ремонтов. Поэтому уже на ранних стадиях проектирования важно оценить надежность объекта, выявить наиболее ненадежные узлы и детали, определить наиболее эффективные меры повышения показателей надежности. Решение этих задач возможно после пред- варительного структурно - логического анализа системы.
Большинство технических объектов, в том числе РЭС, являются сложными системами, состоящими из отдельных узлов, деталей, агрегатов, устройств контроля, управления и т.д.. Техническая система (ТС) - совокупность технических устройств (элементов), предназначенных для выполнения определенной функции или функций. Соответственно, элемент - составная часть системы.
Расчленение ТС на элементы достаточно условно и зависит от постановки задачи расчета надежности. Например при анализе работоспособности технологической линии ее элементами могут считаться отдельные установки и станки, транспортные и загрузочные устройства и т.д.. В свою очередь станки и устройства также могут считаться техническими системами и при оценке их надежности должны быть разделены на элементы - узлы, блоки, которые, в свою очередь - на детали и т.д..
При определении структуры ТС в первую очередь необходимо оценить влияние каждого элемента и его работоспособности на работоспособность системы в целом. С этой точки зрения целесообразно разделить все элементы на четыре группы:
1. Элементы, отказ которых практически не влияет на работоспособность системы (например, деформация кожуха, изменение окраски поверхности и т.п.).
2. Элементы, работоспособность которых за время эксплуатации практически не изменяется и вероятность безотказной работы близка к единице (корпусные детали, малонагруженные элементы с большим запасом прочности).
3. Элементы, ремонт или регулировка которых возможна при работе изделия или во время планового технического обслуживания (наладка или замена технологического инструмента оборудования, настройка частоты селек-тивных цепей РЭС и т.д.).
4. Элементы, отказ которых сам по себе или в сочетании с отказами других элементов приводит к отказу системы.
Очевидно, при анализе надежности ТС имеет смысл включать в рас-смотрение только элементы последней группы.
Для расчетов параметров надежности удобно использовать структурно - логические схемы надежности ТС, которые графически отображают взаимосвязь элементов и их влияние на работоспособность системы в целом. Структурно - логическая схема представляет собой совокупность ранее выделенных элементов, соединенных друг с другом последовательно или параллельно. Критерием для определения вида соединения элементов (последовательного илипараллельного) при построении схемы является влияние их отказа на работоспособность ТС.
Последовательным (с точки зрения надежности) считается соединение, при котором отказ любого элемента приводит к отказу всей системы (рис. 2.1).
Параллельным (с точки зрения надежности) считается соединение, при котором отказ любого элемента не приводит к отказу системы, пока не откажут все соединенные элементы (рис. 2.2).

Определенная аналогия здесь прослеживается с цепью, составленной из проводящих элементов (исправный элемент пропускает ток, отказавший не пропускает): работоспособному состоянию ТС соответствует возможность протекания тока от входа до выхода цепи.
Примером последовательного соединения элементов структурно - логической схемы может быть технологическая линия, в которой происходит переработка сырья в готовый продукт, или РЭС, в котором последовательно осуществляется преобразование входного сигнала. Если же на некоторых участках линии, или пути сигнала, предусмотрена одновременная обработка на нескольких единицах оборудования, то такие элементы (единицы оборудова-ния) могут считаться соединенными параллельно.
Однако не всегда структурная схема надежности аналогична конструктив-ной или электрической схеме расположения элементов. Например, подшипники на валу редуктора работают конструктивно параллельно друг с другом, однако выход из строя любого из них приводит к отказу системы. Аналогично дейст-вие индуктивности и емкости параллельного колебательного контура в селективных каскадах РЭС. Указанные элементы с точки зрения надежности образуют последовательное соединение.
Кроме того, на структуру схемы надежности может оказывать влияние и вид возникающих отказов. Например, в электрических системах для повыше-ния надежности в ряде случаев применяют параллельное или последовательное соединение коммутирующих элементов (рис. 2.3). Отказ таких изделий может происходить по двум причинам: обрыва (т.е. невозможности замыкания цепи) и замыкания (т.е. невозможности разрыва соединения). В случае отказа типа “обрыв” схема надежности соответствует электрической схеме системы (при “обрыве” любого коммутатора при последовательном их соединении возникает отказ, при параллельном - все функции управления будет выполнять исправный коммутатор). В случае отказа типа “замыкание” схема надежности противоположна электрической (в параллельном включении утратится возможность отк-лючения тока, а в последовательном общего отказа не происходит).
|
Структурная схема надежности при отказе типа |
|
Рис. 2.3. Электрические и структурные схемы соединения коммутационных элементов при различных видах отказов
В целом анализ структурной надежности ТС, как правило, включает следующие операции:
1. Анализируются устройства и выполняемые системой и ее составными частями функции, а также взаимосвязь составных частей.
2. Формируется содержание понятия “безотказной работы” для данной конкретной системы.
3. Определяются возможные отказы составных частей и системы, их причины и возможные последствия.
4. Оценивается влияние отказов составных частей системы на ее работоспособность.
5. Система разделяется на элементы, показатели надежности которых известны.
6. Составляется структурно - логическая схема надежности технической системы, которая является моделью ее безотказной работы.
7. Составляются расчётные зависимости для определения показателей надёжности ТС с использованием данных по надежности её элементов и с учётом структурной схемы.
В зависимости от поставленной задачи на основании результатов расчета характеристик надежности ТС делаются выводы и принимаются решения о необходимости изменения или доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д..
3. РАСЧЕТЫ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМ
Расчеты показателей безотказности ТС обычно проводятся в предпо-ложении, что как вся система, так и любой ее элемент могут находиться только в одном из двух возможных состояний - работоспособном и неработоспособном и отказы элементов независимы друг от друга. Состояние системы (рабо-тоспособное или неработоспособное) определяется состоянием элементов и их сочетанием. Поэтому теоретически возможно расчет безотказности любой ТС свести к перебору всех возможных комбинаций состояний элементов, определению вероятности каждого из них и сложению вероятностей рабо-тоспособных состояний системы.
Такой метод (метод прямого перебора - см. п. 3.3) практически универсален и может использоваться при расчете любых ТС. Однако при большом количестве элементов системы n такой путь становится нереальным из-за большого объема вычислений (например, при n=10 число возможных состояний системы составляет,
= 1024, при n=20 превышает , при n=30 -более ). Поэтому на практике используют более эффективные и экономичные методы расчета, не связанные с большим объемом вычислений. Возможность применения таких методов связана со структурой ТС.3.1. Системы с последовательным соединением элементов
Системой с последовательным соединением элементов называется система, в которой отказ любого элемента приводит к отказу всей системы (см. п. 2, рис 2.1). Такое соединение элементов в технике встречается наиболее часто, поэтому его называют основным соединением .
В системе с последовательным соединением для безотказной работы в течении некоторой наработки t необходимо и достаточно, чтобы каждый из ее n элементов работал безотказно в течении этой наработки. Считая отказы элементов независимыми, вероятность одновременной безотказной работы n элементов определяется по теореме умножения вероятностей: вероятность совместного появления независимых событий равна произведению вероятностей этих событий:
(3.1) (3.2)Если система состоит из равнонадёжных элементов (
), то (3.3)Из формул (3.1) - (3.3) очевидно, что даже при высокой надежности элементов надежность системы при последовательном соединении оказывается тем более низкой, чем больше число элементов (например, при
и имеем , при , а при ). Кроме того, поскольку все сомножителив правой части выражения (3.1) не превышают единицы, вероятность безотказной работы ТС при последовательном соединении не может быть выше вероятности безотказной работы самого ненадежного из ее элементов (принцип “хуже худшего”) и из малонадежных элементов нельзя создать высоконадежной ТС с последовательным соединением.Если все элементы системы работают в периоде нормальной эксплуа-тации и имеет место простейший поток отказов (см. п. 1), наработки элементов и системы подчиняются экспоненциальному распределению (1.7) и на основании (3.1) можно записать
(3.4) (3.5)есть интенсивность отказов системы. Таким образом, интенсивность отказов системы при последовательном соединении элементов и простейшем потоке отказов равна сумме интенсивностей отказов элементов. С помощью выраже-ний (1.8) и (1.9) могут быть определены средняя и
- процентная наработки.Из (3.4) - (3.5) следует, что для системы из n равнонадёжных элементов(
)т.е. интенсивность отказов в n раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента.
3.2. Системы с параллельным соединением элементов
Системой с параллельным соединением элементов называется система, отказ которой происходит только в случае отказа всех ее элементов (см. п. 2, рис. 2.2). Такие схемы надежности характерны для ТС, в которых элементы дублируются или резервируются, т.е. параллельное соединение используется как метод повышения надежности (см. п. 4.2). Однако такие системы встречаются и самостоятельно (например, системы двигателей четырехмоторного самолета или параллельное включение диодов в мощных выпрямителях).
Для отказа системы с параллельным соединением элементов в течение наработки t необходимо и достаточно, чтобы все ее элементы отказали в течение этой наработки. Так что отказ системы заключается в совместном отказе всех элементов, вероятность чего (при допущении независимости отказов) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказа элементов:
 (3.7)
(3.7)
Соответственно, вероятность безотказной работы
 (3.8)
(3.8)
Для систем из равнонадежных элементов (
) (3.9)т.е. надежность системы с параллельным соединением повышается при увеличении числа элементов (например, при
и , а при ).Поскольку
, произведение в правой части (3.7) всегда меньше любого из сомножителей, т.е. вероятность отказа системы не может быть выше вероятности самого надежного ее элемента (“лучше лучшего”) и даже из сравнительно ненадежных элементов возможно построение вполне надежной системы.При экспоненциальном распределении наработки (1.7) выражение (3.9) принимает вид
(3.10)откуда с помощью (1.1) после интегрирования и преобразований средняя наработка системы определяется
 (3.11)
-
средняя наработка
элемента. При
больших значениях
n справедлива
приближенная
формула
(3.11)
-
средняя наработка
элемента. При
больших значениях
n справедлива
приближенная
формула
 (3.12)
(3.12)
Таким образом, средняя наработка системы с параллельным соединением больше средней наработки ее элементов (например, при
, при ).3.3. Системы типа “m из n”
Систему типа “m из n” можно рассматривать как вариант системы с параллельным соединением элементов, отказ которой произойдет, если из n элементов, соединенных параллельно, работоспособными окажутся менее m элементов (m

На рис. 3.1 представлена система “2 из 5”, которая работоспособна, если из пяти её элементов работают любые два, три, четыре или все пять (на схеме пунктиром обведены функционально необходимые два элемента, причем выделение элементов 1 и 2 произведено условно, в действительности все пять элементовравнозначны). Системы типа “m из n” наиболее часто встречаются в электрических и связных системах (при этом элементами выступают связую-щие каналы), технологических линий, а также при структурном резервировании (см. п. 4.1, 4.2).
Для расчета надежности систем типа “m из n“ при сравнительно небольшом количестве элементов можно воспользоваться методом прямого перебора . Он заключается в определении работоспособности каждого из возможных состояний системы, которые определяются различными сочета-ниями работоспособных и неработоспособных состояний элементов.
Все состояния системы “2 из 5“ занесены в табл. 3.1. (в таблице работоспособные состояния элементов и системы отмечены знаком “+“, неработоспособные - знаком “-“). Для данной системы работоспособность определяется лишь количеством работоспособных элементов. По теореме умножения вероятностей вероятность любого состояния определяется как произведение вероятностей состояний, в которых пребывают элементы. Например, в строке 9 описано состояние системы, в которой отказали элементы 2 и 5, а остальные работоспособны. При этом условие “2 из 5“ выполняется, так что система в целом работоспособна. Вероятность такого состояния
(предполагается, что все элементы равнонадежны). С учетом всех возможных состояний вероятность безотказной работы системы может быть найдена по теореме сложения вероятностей всех работоспособных сочетаний. Поскольку в табл. 3.1 количество неработоспособных состояний меньше, чем работоспособных (соответственно 6 и 26), проще вычислить вероятность отказа системы. Для этого суммируются вероятности неработоспособных состояний (где не выполняется условие “ 2 из 5 “)
(3.13)Тогда вероятность безотказной работы системы
(3.14)Расчет надежности системы “m из n“ может производиться комбинаторным методом , в основе которого лежит формула биномиального распределения. Биномиальному распределению подчиняется дискретная случайная величина k - число появлений некоторого события в серии из n опытов, если в отдельном опыте вероятность появления события составляет p. При этом вероятность появления события ровно k раз определяется
 (3.16)
(3.16)
Значения биномиальных коэффициентов приведены в приложении.
Поскольку для отказа системы “m из n“ достаточно, чтобы количество исправных элементов было меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0, 1, ... (m-1) :
 (3.17)
(3.17)
Аналогичным образом можно найти вероятность безотказной работы как сумму (3.15) для k=m, m+1, ... , n :
 (3.18)
(3.18)Таблица 3.1
Таблица состояний системы “2 из 5”
| Состояние элементов | Состояние Вероятность||||
Очевидно, что Q+P=1 , поэтому в расчетах следует выбирать ту из формул (3.17), (3.18), которая в данном конкретном случае содержит меньшее число слагаемых.
Для системы “2 из 5“ (рис. 3.1) по формуле (3.18) получим:
(3.19)Вероятность отказа той же системы по (3.17):
(3.20)что, как видно, дает тот же результат для вероятности безотказной работы.
В табл. 3.2 приведены формулы для расчета вероятности безотказной работы систем типа “m из n“ при mm=1 система превращается в обычную систему с параллельным соединением элементов, а при m = n - с последовательным соединением.
Таблица 3.2
| Общее число элементов, n | |||||
3.4. Мостиковые схемы
Мостиковая структура (рис. 3.2, а, б) не сводится к параллельному или последовательному типу соединения элементов, а представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (элемент 3 на рис. 3.2, а, элементы 3 и 6 на рис. 3.2, б). Работоспособность такой системы определяется не только количеством отказавших элементов, но и их положением в структурной схеме. Например, работоспособность ТС, схема которой приведена на рис. 3.2, а, будет утрачена при одновременном отказе элементов 1 и 2, или 4 и 5, или 2, 3 и 4 и т.д.. В то же время отказ элементов 1 и 5, или 2 и 4, или 1, 3 и 4, или 2, 3 и 5 к отказу системы не приводит.

Таблица 3.3
Таблица состояний мостиковой системы
| Состояние элементов | СостояниеВероятность состояния | |||||
Для расчета надежности мостиковых систем можно воспользоваться методом прямого перебора , как это было сделано для систем “m из n“ (п. 3.3), но при анализе работоспособности каждого состояния системы необходимо учитывать не только число отказавших элементов, но и их положение в схеме (табл. 3.3). Вероятность безотказной работы системы определяется как сумма вероятностей всех работоспособных состояний:
 (3.21)
(3.21)
В случае равнонадёжных элементов
(3.22)Метод прямого перебора эффективен только при малом количестве элементов n , о чем говорилось в начале разд. 3, поскольку число состояний системы составляет
. Например, для схемы на рис. 3.2,б их количество составит уже 256. Некоторое упрощение достигается, если в таблицу состояний включать только сочетания, отвечающие работоспособному (или только неработоспособному) состоянию системы в целом.Для анализа надежности ТС, структурные схемы которых не сводятся к параллельному или последовательному типу, можно воспользоваться также методом логических схем с применением алгебры логики (булевой алгебры). Применение этого метода сводится к составлению для ТС формулы алгебры логики, которая определяет условие работоспособности системы. При этом для каждого элемента и системы в целом рассматриваются два противоположных события - отказ и сохранение работоспособности.
Для составления логической схемы можно воспользоваться двумя методами - минимальных путей и минимальных сечений.
Рассмотрим метод минимальных путей для расчета вероятности безотказной работы на примере мостиковой схемы (рис. 3.2,а).
Минимальным путем называется последовательный набор работоспо-собных элементов системы, который обеспечивает ее работоспособность, а отказ любого из них приводит к ее отказу.
Минимальных путей в системе может быть один или несколько. Очевидно, система с последовательным соединением элементов (рис. 2.1) имеет только один минимальный путь, включающий все элементы. В системе с параллельным соединением (рис. 2.2) число минимальных путей совпадает с числом элементов и каждый путь включает один из них.
Для мостиковой системы из пяти элементов (рис. 3.2,а) минимальных путей четыре: (элементы 1 и 4), (2 и 5), (1, 3 и 5), (2, 3 и 5). Логическая схема такой системы (рис. 3.3) составляется таким образом, чтобы все элементы каждого минимального пути были соединены друг с другом последовательно, а все минимальные пути параллельно.

Затем для логической схемы составляется функция алгебры логики А по общим правилам расчета вероятности безотказной работы, но вместо символов вероятностей безотказной работы элементов
и системы Р используются символы события (сохранения работоспособности элемента ai и системы А). Так, “отказ“ логической схемы рис. 3.3 состоит в одновременном отказе всех четырех параллельных ветвей, а “безотказная работа” каждой ветви - в одновременной безотказной работе ее элементов. Последовательное соединение элементов логической схемы соответствует логическому умножению (“И”), параллельное - логическому сложению (“ИЛИ”). Следовательно, схема рис. 3.3 соответствует утверждению: система работоспособна, если работоспособны элементы 1 и 4, или 2 и 5, или 1,3 и 5, или 2,3 и 4. Функция алгебры логики запишется: (3.23)В выражении (3.23) переменные а рассматриваются как булевы, т.е. могут приниматься только два значения: 0 или 1. Тогда при возведении в любую степень k любая переменная a сохраняет свое значение:
. На основе этого свойства функция алгебры логики (3.23) может быть преобразована к виду (3.24)Заменив в выражении (3.24) символы событий
их вероятностями , получим уравнение для определения вероятности безотказной работы системы (3.25)Для системы равнонадёжных элементов (
) выражение (3.25) легко преобразуется в формулу (3.22).Метод минимальных путей дает точное значение только для сравнительно простых систем с небольшим числом элементов. Для более сложных систем результат расчета является нижней границей вероятности безотказной работы.
Для расчета верхней границы вероятности безотказной работы системы служит метод минимальных сечений .
Минимальным сечением называется набор неработоспособных элементов, отказ которых приводит к отказу системы, а восстановление работоспособности любого из них - к восстановлению работоспособности системы. Как и минимальных путей, минимальных сечений может быть несколько. Очевидно, система с параллельным соединением элементов имеет только одно минимальное сечение, включающее все ее элементы (восстановление любого восстановит работоспособность системы). В системе с последовательным соединением элементовчисло минимальных путей совпадает с числом элементов, и каждое сечение включает один из них .
В мостиковой системе (рис. 3.2, а) минимальных сечений четыре (элементы 1 и 2), (4 и 5), (1, 3 и 5) , (2, 3 и 4). Логическая схема системы (рис.3.4) составляется таким образом, чтобы все элементы каждого мини-мального сечения были соединены друг с другом параллельно, а все мини-мальные сечения - последовательно. Аналогично методу минимальных путей, составляется функция алгебры логики. “Безотказная работа” логической системы рис. 3.4 заключается в “безотказной работе” всех последовательных участков, а “отказ” каждого из них - в одновременном “отказе” всех парал-лельно включенных элементов. Как видно, поскольку схема метода минимальных сечений формулирует условия отказа системы, в ней последо-вательное соединение соответствует логическому “ИЛИ”, а параллельное - логическому “И”. Схема рис. 3.4 соответствует формулировке: система отка-жет, если откажут элементы 1 и 2, или 4 и 5, или 1, 3 и 5, или 2, 3 и 4. Функция алгебры логики запишется
(3.26)После преобразований с использованием свойств булевых переменных (3.26) приобретает форму (3.24), после замены событий их вероятностями переходит в выражение (3.25).
Таким образом, для мостиковой системы из пяти элементов верхняя и нижняя границы вероятности безотказной работы, полученные методами минимальных сечений и минимальных путей, совпали с точными значениями (3.22), полученными методом прямого перебора. Для сложных систем это может не произойти, поэтому методы минимальных путей и минимальных сечений следует применять совместно.
В ряде случаев анализа надежности ТС удается воспользоваться методом разложения относительно особого элемента , основанными на известной в математической логике теореме о разложении функции логики по любому аргументу.Согласно ей, можно записать:
(3.27) и - вероятности безотказной работы и отказа i - го элемента, и-вероятности работоспособного состояния системы при условии, что i - й элемент абсолютно надежен и что i - й элемент отказал.Для мостиковой схемы (рис. 3.2, а) в качестве особого элемента целесообразно выбрать диагональный элемент 3. При
мостиковая схема превращается в параллельно - последовательное соединение (рис. 3.5, а), а при - в последовательно - параллельное (рис. 3.5, б).
Для преобразованных схем можно записать:
(3.28) (3.29)Тогда на основании формулы (3.27) получим:
(3.30)Легко убедиться, что для равнонадёжных элементов формула (3.30) об-ращается в (3.22).
Этим методом можно воспользоваться и при разложении относительно нескольких “особых” элементов. Например, для двух элементов (i, j ) выражение (3.27) примет вид:
(3.31)Вероятность безотказной работы мостиковой схемы (рис. 3.2, б) при разложении относительно диагональных элементов 3 и 6 по (3.31) определится:
(3.32)Вероятности
легко ставить, выполнив предварительно преобразованные схемы, подобно рис. 3.5, а, б.3.5. Комбинированные системы
Большинство реальных ТС имеет сложную комбинированную структуру , часть элементов которой образует последовательное соединение, другая часть - параллельное, отдельные ветви элементы или ветви структуры образуют мостиковые схемы или типа “m из n”.
Метод прямого перебора для таких систем оказывается практически не реализуем. Более целесообразно в этих случаях предварительно произвести декомпозицию системы, разбив ее на простые подсистемы - группы элементов, методика расчета надежности которых известна. Затем эти подсистемы в структурной схеме надежности заменяются квазиэлементами с вероятностями безотказной работы, равными вычисленным вероятностям безотказной работы этих подсистем. При необходимости такую процедуру можно выполнить несколько раз, до тех пор, пока оставшиеся квазиэлементы не образуют структуру, методика расчета надежности которой также известна.

В качестве примера рассмотрим комбинированную систему, представленную на рис. 3.6. Здесь элементы 2 и 5, 4 и 7, 9 и 12, 11 и 14 попарно образуют друг с другом последовательные соединения. Заменим их соответственно квазиэлементами А, В, С, Д, для которых расчет надежности элементарно выполняется по формулам п. 3.1. Элементы 15, 16, 17 и 18 образуют параллельное соединение (п. 3.2), а элементы 3, 6, 8, 10 и 13 - систему “3 из 5” (п. 3.2). Соответствующие квазиэлементы обозначим E и F. В результате преобразованная схема примет вид, показанный на рис. 3.7, а. В ней в свою очередь элементы А, В, С, Д, F образуют мостиковую схему (п. 3.4), которую заменяем квазиэлементом 6. Схема, полученная после таких преобразований (рис.3.7,б), образует последовательное соединение элементов 1, G, E, 19, для которых справедливы соотношения п. 3.1. Отметим, что метод прямого перебора для исходной системы потребовал бы рассмотреть
возможных состояний.4. ПОВЫШЕНИЕ НАДЕЖНОСТИ ТЕХНИЧЕСКИХ СИСТЕМ
4.1. Методы повышения надежности
Расчетные зависимости для определения основных характеристик надежности ТС показывают, что надежность системы зависит от ее структуры (структурно - логической схемы) и надежности элементов. Поэтому для сложных систем возможны два пути повышения надежности: повышение надежности элементов и изменение структурной схемы.
Повышение надежности элементов на первый взгляд представляется наиболее простым приемом повышения надежности системы. Действительно, теоретически всегда можно указать такие характеристики надежности элемен-тов, чтобы вероятность безотказной работы системы удовлетворяла заданным требованиям. Однако практическая реализация такой высокой надежности элементов может оказаться невозможной. Рассмотрение методов обеспечения надежности элементов ТС является предметом специальных технологических и физико-химических дисциплин и выходит за рамки теории надежности. Однако, в любом случае, высоконадежные элементы, как правило, имеют большие габариты, массу и стоимость. Исключение составляет использование более совершенной элементной базы, реализуемой на принципиально новых физических и технологических принципах (например, в РЭС - переход от дискретных элементов на интегральные схемы).
Изменение структуры системы с целью повышения надежности подразумевает два аспекта.
С одной стороны, это означает перестройку конструктивной или функциональной схемы ТС (структуры связей между составными элементами), изменение принципов функционирования отдельных частей системы (например, переход от аналоговой обработки сигналов к цифровой). Такого рода преобразования ТС возможны исключительно редко, так что этот прием, в общем, не решает проблемы надежности.
С другой стороны, изменение структуры понимается как введение в ТС дополнительных, избыточных элементов, включающихся в работу при отказе основных. Применение дополнительных средств и возможностей с целью сохранения работоспособного состояния объекта при отказе одного или нескольких его элементов называется резервированием .
Принцип резервирования подобен рассмотренному ранее параллельному соединению элементов (п. 3.2) и соединению типа “n из m” (п. 3.3), где за счет избыточности возможно обеспечение более высокой надежности системы, чем ее элементов.
Выделяют несколько видов резервирования (временное, информацион-ное, функциональное и др.). Для анализа структурной надежности ТС интерес представляет структурное резервирование - введение в структуру объекта дополнительных элементов, выполняющих функции основных элементов в случае их отказа.
Классификация различных способов структурного резервирования осуществляется по следующим признакам:
1) по схеме включения резерва:
Общее резервирование, при котором резервируется объект в целом;
Раздельное резервирование, при котором резервируются отдельные элементы или их группы;
Смешанное резервирование, при котором различные виды резервирования сочетаются в одном объекте;
2) по способу включения резерва:
Постоянное резервирование, без перестройки структуры объекта при возникновении отказа его элемента;
Динамическое резервирование, при котором при отказе элемента происходит перестройка структуры схемы. В свою очередь подразделяется на:
а) резервирование замещением, при котором функции основного элемента передаются резервному только после отказа основного;
б) скользящее резервирование, при котором несколько основных элементов резервируется одним или несколькими резервными, каждый из которых может заменить любой основной (т.е. группы основных и резервных элементов идентичны).
3) по состоянию резерва:
Нагруженное резервирование, при котором резервные элементы (или один из них) находятся в режиме основного элемента;
Облегченное резервирование, при котором резервные элементы (по крайней мере один из них) находятся в менее нагруженном режиме по сравнению с основными;
Ненагруженное резервирование, при котором резервные элементы до начала выполнения ими функций находятся в ненагруженном режиме.
Основной характеристикой структурного резервирования является кратность резервирования - отношение числа резервных элементов к числу резервируемых ими основных элементов, выраженное несокращаемой дробью (типа 2:3; 4:2 и т.д.). Резервирование одного основного элемента одним резервным (т.е. с кратностью 1:1) называется дублированием .
Количественно повышение надежности системы в результате резервирования или применения высоконадежных элементов можно оценить по коэффициенту выигрыша надежности , определяемому как отношение показателя надежности до и после преобразования системы. Например, для системы из n последовательно соединенных элементов после резервирования одного из элементов (k-го) аналогичным по надежности элементом коэффициент выигрыша надежности по вероятности безотказной работы составит
(4.1)Из формулы (4.1) следует, что эффективность резервирования (или другого приема повышения надежности) тем больше, чем меньше надежность резервируемого элемента (при
, при ). Следова-тельно, при структурном резервировании максимального эффекта можно до-биться при резервировании самых ненадежных элементов (или групп элемен-тов).В общем случае при выборе элемента (или группы элементов) для повышения надежности или резервирования необходимо исходить из условия обеспечения при этом максимального эффекта. Например, для мостиковойсхемы (рис. 3.2,а) из формулы (3.21) можно получить выражение для частных производных вероятности безотказной работы системы по вероятности безотказной работы каждого из элементов, которые для идентичных по надежности элементов принимают следующий вид:
(4.2)Очевидно, максимальное увеличение надежности системы обеспечит увеличение надежности или резервирование того элемента, частная производная для которого при данных условиях принимает максимально положительное значение. Сравнение выражений (4.2) и (4.3) показывает, что при любых положительных значениях p и q выражение (4.2) больше выражения (4.3) и, следовательно, в мостиковой схеме с идентичными элементами эффективность повышения надежности или резервирования “периферийных” элементов 1, 2, 4 и 5 (см. рис. 3.2, а) выше, чем диагонального элемента 3, если в качестве критерия эффективности взять вероятность безотказной работы.
Таким образом, наибольшее влияние на надежность системы оказывают элементы, обладающие высоким значением производной
, а при последова-тельном соединении - наименее надежные.В более сложных случаях для выбора элементов, подлежащих изменению, используются как аналитические, так и численные методы оптимизации надежности.
4.2. Расчет надежности систем с резервированием
Расчет количественных характеристик надежности систем с резервированием отдельных элементов или групп элементов во многом определяется видом резервирования. Ниже рассматриваются схемы расчетов для самых распространенных случаев простого резервирования, к которым путем преобразований может быть приведена и структура смешенного резервирования. При этом расчетные зависимости получены без учета надежности переключающих устройств, обеспечивающих перераспределение нагрузки между основными и резервными элементами (т.е. для “идеальных” переключателей). В реальных условиях введение переключателей в структурную схему необходимо учитывать и в расчете надежности систем.
Расчет систем с нагруженным резервированием осуществляется по формулам последовательного и параллельного соединения элементов аналогично расчету комбинированных систем (п. 3.5). При этом считается, что резервные элементы работают в режиме основных как до, так и после их отказа, поэтому надежность резервных элементов не зависит от момента их перехода из резервного состояния в основное и равна надежности основных элементов.
Для системы с последовательным соединением n элементов (рис. 2.1) при общем резервировании с кратностью l (рис. 4.1, а)
 (4.4)
(4.4)
В частности, при дублировании (l =1)
(4.5)При раздельном резервировании (рис. 4.1,б)
 (4.6)
(4.6)
а при раздельном дублировании (l =1)
(4.7)
Тогда коэффициенты выигрыша надежности по вероятности безотказной работы при дублировании
(4.8)откуда следует, что раздельное резервирование эффективнее общего (например, для системы из трех одинаковых элементов при
, .При ненагруженном резервировании резервные элементы последовательно включаются в работу при отказе основного, затем первого резервного и т.д. (рис. 4.2), поэтому надежность резервных элементов зависит от момента их перехода в основное состояние. Такое резервирование в различных ТС встречается наиболее часто, т.к. оно по сути аналогично замене отказавших элементов и узлов на запасные.

Если резервные элементы до их включения абсолютно надежны, то для системы с ненагруженным резервированием кратности l (всего элементов l+1 )
(4.9)т.е. вероятность отказа в (l+1 )! раз меньше, чем при нагруженном (параллельном соединении, см. формулу (3.7)).
Для идентичных по надежности основного и резервного элементов
 (4.10)
(4.10)
При экспоненциальном распределении наработки (простейшем потоке отказов, см. 1.7) в случае
можно воспользоваться приближенной формулой (4.11)
(4.11)
При ненагруженном резервировании средняя наработка на отказ
(4.12)а для идентичных элементов
Облегченное резервирование используется при большой инерционности переходных процессов, происходящих в элементе при его переходе из резервного в основной режим, и нецелесообразности применения нагруженного резервирования из - за недостаточного выигрыша в надежности (в РЭС это характерно для устройств на электровакуумных приборах). Очевидно, облегченный резерв занимает промежуточное положение между нагруженным и ненагруженным.
Точные выражения для расчета надежности систем при облегченном резервировании весьма громоздки и неоднозначны, однако при экспонен-циальном распределении наработки справедлива приближенная формула
 (4.13)
- интенсивность
отказов элементов
в облегченном
режиме, l
- кратность
резервирования.
(4.13)
- интенсивность
отказов элементов
в облегченном
режиме, l
- кратность
резервирования.
Скользящее резервирование используется для резервирования нескольких одинаковых элементов системы одним или несколькими одинаковыми резервными (рис. 4.3, здесь все элементы идентичны, а элемент 4 - избыточный). Очевидно, отказ системы произойдет, если из общего количества идентичных элементов (основных и резервных) число отказавших превышает число резервных. Расчет вероятности безотказной работы систем со скользящим резервированием аналогичен расчету систем типа “m из n”, см. п. 3.3.
Задание на курсовую работу (КР) содержит в качестве исходных данных структурную схему надежности технической системы (ТС) и интенсивность отказов ее элементов (см. п. 7). То есть студент оказывается в ситуации, когда выполнены п. 1 - 6 анализа структурной надежности ТС (см. разд. 2), и ему надлежит в первую очередь выполнить п. 7 - составить расчетные зависимости для определения показателей надежности системы для различных значений наработки t , чтобы графически изобразить вероятность безотказной работы P(t) как функцию наработки.
Поскольку заданная схема надежности является комбинированной, ее следует подвергнуть декомпозиции, как это описано в п. 3.5. Далее, вводя соответствующие квазиэлементы, преобразовать исходную схему к простейшему виду и, используя соответствующие формулы п. 3.1 - 3.4, для ряда значений наработки t в предположении простейшего потока отказов формулы (1.7) вычислить значения вероятностей безотказной работы элементов, квазиэлементов и всей системы. В пояснительной записке следует привести все промежуточные преобразования исходной схемы, конкретные рабочие расчетные формулы с их обоснованием, а результаты расчета представить в виде таблицы, в которой по столбцам изменяется значение наработки t , а по строкам в столбцах приводятся вычисленные значения вероятностей безотказной работы элементов, квазиэлементов и всей системы, полученные по рабочим формулам. При этом диапазон измерения наработки t должен обеспечить снижение вероятности безотказной работы системы до уровня 0.1 - 0.2 и содержать не менее 8-10 значений аргумента.
После этого строится график зависимости P(t) по результатам расчета. И него графически по заданному значению
определяется - процентная наработка системы (см. (1.9)), .По заданию требуется предложить способы увеличения
- процентной наработки в 1.5 раза за счет повышения надежности элементов и за счет структурного резервирования.Предварительно следует определить элемент или квазиэлемент окончательно преобразованной схемы, повышение надежности которого даст максимальный эффект в отношении надежности всей системы. Критерии выбора приведены в п. 4.1. Поскольку аналитически определить производные вида (4.2), (4.3) обычно не удается, выбор элемента может быть осуществлен по величине вероятности безотказной работы.
Для дальнейших действий необходимо вычислить требуемое улучшенное значение
- процентной наработки элементарным умножением на 1.5. Следовательно, чтобы удовлетворить заданию в отношении повышения надежности системы, необходимо обеспечить вероятность безотказной работы за время . Теперь следует повторить расчет надежности элементов, квазиэлементов и всей системы за время и дополнить этим столбцом предыдущую таблицу. Зная вероятности безотказной работы всех элементов преобразованной схемы и требуемое значение , легко определить,какую вероятность безотказной работы за время должен иметь квазиэлемент, избранный для модернизации.По первому варианту модернизации необходимо определить интенсивности отказов элементов, входящих в данный квазиэлемент, при которых при неизменной структуре квазиэлемента обеспечивалось бы необходимое значение
. Проще это осуществить графоаналитическим методом, задавая ряд пропорционально уменьшенных (по сравнению с исходной) интенсивностей отказов для составляющих квазиэлемента и просчитывая каждый раз величину . Из построенного по этим данным графика можно определить необходимую кратность снижения интенсивности отказов элементов и сами значения интенсивности. Для найденного решения следует выполнить проверочный расчет вероятности безотказной работы системы за время .По второму методу надежность выбранного квазиэлемента можно повысить за счет резервирования без изменения надежности составляющих элементов. При этом, основываясь на рекомендациях и соображениях, изложенных в п. 4.1, 4.2, учитывая структуру модернизируемого квазиэлемента, нужно выбрать, какие его составляющие элементы и как следует резервировать для достижения наибольшего эффекта. Далее остается определить необходимую кратность резервирования
. Поскольку есть величина дискретная, аналитически ее определить невозможно. Для решения задачи нужно последовательно увеличивать кратность резервирования, начиная с единицы, каждый раз по соответствующим формулам из п. 4.2 определять величину вероятности безотказной работы квазиэлемента в течении времени . Как только необходимое значение будет обеспечено, окажется реализованным второй метод повышения надежности системы. Для найденного решения также необходимо провести проверку вероятности безотказной работы системы за время. Модернизированную структуру с резервированием следует привести в пояснительной записке.Для построения зависимостей вероятностей безотказной работы от времени для модернизированной системы по первому и второму методу удобно дополнить ранее составленную таблицу соответствующими строками. Графики этих зависимостей следует изобразить совместно с кривой P(t ) исходной системы.
Полученное семейство кривых позволяет провести сравнение двух вариантов модернизации, которое следует привести в качестве вывода к работе.
Пояснительная записка должна быть оформлена в соответствии с СТП КрПИ 3.1 - 92 «Текстовые документы. Требования к оформлению». Все действия и использование расчетных сотношений должны быть объяснены и обоснованы. Для заимствуемой информации (формулы, численные значения констант) необходимо указать источник заимствования.
Задания на курсовую работу приведены в разд. 6, а в разд. 7 - пример расчета надежности.
6. ИСХОДНЫЕ ДАННЫЕ К РАБОТЕ
По структурной схеме надежности технической системы в соответствии с вариантом задания, требуемому значению вероятности безотказной работы системы
и значениям интенсивностей отказов ее элементов (табл. 6.1) требуется:1. Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 - 0.2.
2. Определить
- процентную наработку технической системы.3. Обеспечить увеличение
- процентной наработки не менее, чем в 1.5 раза за счет:а) повышения надежности элементов;
б) структурного резервирования элементов системы.
Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.
На схемах обведенные пунктиром m элементов являются функционально необходимыми из n параллельных ветвей.




















7. ПРИМЕР РАСЧЕТА НАДЕЖНОСТИ
Структурная схема надежности приведена на рис 7.1. Значения интенсивности отказов элементов даны в
1/ч.
1. В исходной схеме элементы 2 и 3 образуют параллельное соединение. Заменяем их квазиэлементом А. Учитывая, что
, получим . (7.1)2. Элементы 4 и 5 также образуют параллельное соединение, заменив которое элементом В и учитывая, что
, получим . (7.2)3. Элементы 6 и 7 в исходной схеме соединены последовательно. Заменяем их элементом С, для которого при
4. Элементы 8 и 9 образуют параллельное соединение. Заменяем их элементом D, для которого при
, получим . (7.4)5. Элементы 10 и 11 с параллельным соединением заменяем элементом Е, причем, так как
, то (7.5)6. Элементы 12 , 13 , 14 и 15 образуют соединение “2 из 4”, которое заменяем элементом F. Так как
 (7.6)
(7.6) 
7. Преобразованная схема изображена на рис. 7.2.
8. Элементы A, B, C, D и Е образуют (рис. 7.2) мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента (см. раздел 3.4), в качестве которого выберем элемент С. Тогда
(7.7) - вероятность безотказной работы мостиковой схемы при абсолютно надежном элементе С (рис. 7.3, а), - вероятность безотказной работы мостиковой схемы при отказавшем элементе С (рис. 7.3, б).
Учитывая, что
, получим (7.8)
(7.8)
9. После преобразований схема изображена на рис. 7.4.
 10.
В преобразованной
схеме (рис.
7.4) элементы 1, G и
F образуют
последовательное
соединение.
Тогда вероятность
безотказной
работы всей
системы
(7.9)
10.
В преобразованной
схеме (рис.
7.4) элементы 1, G и
F образуют
последовательное
соединение.
Тогда вероятность
безотказной
работы всей
системы
(7.9)
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 7.1) подчиняются экспоненциальному закону.
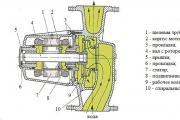
Многие факторы которые влияют на оборудование систем, классифицируют по области их действия, это показано на рис.1. В зависимости от типа оборудования на которых влияют факторы влияющие на надежность, могут изменяться.
Рисунок — 1
Конструктивные факторы:
- определение составных элементов и материалов;
- выбор функциональной и структурной схем, варианты контроля резервирования;
- выбор условий и режимов работы элементов в системе;
- выбор защит и установок на технологические параметры элементов;
- принятие во внимание психофизиологических характеристик сотрудников;
- Создание документации.
К производственным факторам относятся:
- контроль качества элементов и метериалов которые приходят от поставщиков;
- контроль качества элементов на всех этапах процесса создания (точность, прочность, характеристика объектов и тд.);
- организация процесса создание или настройки оборудования;
- квалификация изготовителей;
- условие работы на предприятии;
- контроль наладки и монатажа оборудования систем.
Эксплуатационные факторы , это факторы которые находятся вне зоны производства и проектирования объектов. Они могут быть объективные и субъективные. Объективные факторы оказывают влияние на надежность объектов. Они бывают внутренние и внешние.
Внешние факторы обусловленны условиями применения и внешней средой. К таким можно отнести климатические факторы (разные температуры, радиация, влажность), электромагнитные излучения, механические воздействия (вибрации, удары). Внутренние факторы же обусловленны с изменением характеристик самых объъектов и их несущих материалов, это износ, старение, коррозия. Эти изменения реализуются в течении времени. Климатические условия показаны на рис.2.

Рисунок — 2
Субъективные факторы подразумевают:
- обучееность сотрудников;
- квалификация сотрудников;
- способы и средства организации объектов;
- анализ и организация сбора о надежности объектов;
Классификация методов расчета систем на надежность
Рассчитать систему на надежность — это определить одну или пару параметров надежности. Такие расчеты используют на разных этапах разработки, эксплуатации и создания объектов. Основные факторы при выборе метода расчета:
- особенности отказов элементов в системе;
- этап создание системы;
- вариант подключение элементов в системе;
- тип закона распределений времени безотказной работы;
- восстанавливаемость объекта;
- режим работы системы и элементов;
- средства анализа объекта.
На этапе эксплуатации и создания расчеты проводят по результатам эксплуатации и испытаний. По принципу отказов элементов различают разные методы расчета, при постепенных, внезапных и перемежающихся. В зависимости от метода осмотра объекта есть два класса расчета надежности: функциональные и структурные. При структурной схеме расчитывают показатели надежности объекта, элементов и связей между ними. Функциональная схема — определяется надежность заданных функций между элементами.
Расчет надежности при основном соединении элементов в системе
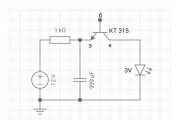
Основным соединением элементов в системе характеризует такое соединение, при котором отказ любого элемента системы призводит к отказу всей системы. Схема показана на рис.3.
![]()
Рисунок — 3
Порядок расчета надежности.
- Создание понятие отказа объекта.
- Создание схемы расчета надежности. В схеме нужно указывать время работы каждого блока.
- Нада составить таблицу, которая показана на рис.4.
- Расчет параметров надежности.
- Рекомендации направленные на улучшения надежности объекта.
При расчете надежности нужно перемножать вероятности безотказной работы отдельных элементов. Считается по формулам, которые показаны на рис.5.

Рисунок — 4

Рисунок — 5
Показатели надежности объектов
Надежность
— это характеристика объекта сохранять со временем в назначенных рамках значений всех характеристик, которые обозначают способность реализовывать нужные функции в нужных условиях и режимах.
Можно подчеркнуть следующие особенности. Во-первых, выполнение объектом заданных функций должна быть непрерывной на протяжении некоторого времени. Нет смысла говорить о надежности объекта, при таких работах как ремонт, замена, другие одиночные мероприятия. Во-вторых, в понятие надежность подразумевается также определенные пределы
. При отказе некоторых элементов системы, система работает но с меньшой мощностью в заданных пределах. Также один и тот же элемент может выполнять в разное время разные функции. Его надежность в разных случаях будет разной. Элемент
— в некой степени ограниченных объект, которые является частью другого объекта. Понятие элемент
и системы
, относительны, ибо каждый объект в разных ситуациях может быть или тем или другим.
Надежность как сложный параметр зависит от условий и назначений объекта. Также зависит от — ремонтопригодности, безотказности, сохраняемости и долговечности. Безотказность — это один из самых важных параметров надежности систем и элементов. Это параметр характеризующий объектов сохранять работоспособность на промежутке времени. Безотказность описывается техническим состоянием объекта, это работоспособность, исправность, дефекты, повреждения и отказ. Исправное состояние — это такое состояние объекта, при котором соблюдены все требование конструкторской и нормативно-технической документации. При работоспособном состоянии объекта характеристики которые определяют способность делать заданные функции, тоже соответствуют документации. Границы между неисправным и исправным, между неработоспособными и работоспособными состояниями традиционно условные, и подразумевают набор параметров которым должны соответстовать элементы или система.
Переход объектов из разных состояний обычно происходит после отказа или повреждения. Схема событий и состояний показана на рис.6. Работоспособный объект в отличии от исправного должен отвечать только лиш требованием документации. Термин дефект , применяется в основном на этапах ремонта или изготовления. Неисправность же, применяется при эксплуатации объектов. Ремонтопригодность — это характеристика объекта, которая реализуется к предупреждению и обнаружению причин отказов.

Рисунок — 6
Для множества объектов характеристика восстонавливаемости нужно рассматривать на всем этапе существования. При решении задач обеспечения, оценивая и прогнозирования надежности существенное решение имеет ответ на вопрос отказа объекта — восстанавливать его или нет. При ответе на вопрос ведется череда событий по поводу показателей надежности. Долговечность — это характеристика объекта держать работоспособное состояние до подхода предельного состояния при установленной системе технического ремонта или обслуживания. смена состояния объекта в предельное, влечет за собой временное или окончательное прекращение его эксплуатации.
наработка — продолжительность работы объекта. Измеряется в единицах времени или единицах объема сделанной работы. Наработка до отказа — это наработка объекта от начала до возникновения первого отказа при эксплуатации. Наработка до отказа описывает безотказность как для ремонтируемых и не ремонтируемых объектов. Физический смысл ресурса — область возможной наработки объекта. Для неремонтируемых частей он одинаковый с запасом нахождения в работоспособном состоянии при эксплуатации. Как любая случайная величина, ресурс характеризуется распределением вероятностей. Сохраняемость — это характеристика объекта сохранять значения показателей безотказности, ремонтопригодности и долговечности в течении эксплуатации.
Разрабатываемая система в конечном варианте будет представлять собой Web - приложение. Таким образом, для обеспечения надежной работы системы необходимо обеспечить надежную работу программной части. При этом надежность системы будет рассчитываться по формуле (1):
Р сист = Р апп.ч Р прог.ч , (1)
где Р сист - надежность всей системы;
Р апп.ч - надежность аппаратной части;
Р прог.ч - надежность программной части.
Расчет надежности программной части
Надежность программной части будет рассчитываться по формуле (2):
Р прог.ч = Р сервер Р клиент P ПО , (2)
где Р сервер - надежность программного обеспечения сервера;
Р клиент - надежность программного обеспечения клиента;
Р ПО - надежность разработанного программного обеспечения.
Расчет надежности программного обеспечения сервера
Надежность программного обеспечения сервера рассчитывается по формуле(3):
Р сервер = Р СУБД Р ОС , (3)
где РСУБД - надежность системы управления базой данных;
Р ОС - надежность операционной системы, установленной на сервере.
В качестве операционной системы, установленной на сервере, используется Red Hat Enterprise Linux 5, компания производитель установила вероятность безотказной работы равной:
Р ОС = 0,99.
В качестве сервера базы данных используется СУБД Cache, компания производитель Intersystems установила вероятность безотказной работы равной:
Р СУБД = 0,98.
Таким образом, вероятность безотказной работы ПО сервера составляет:
Р сервер =0,99 0,98= 0,98
Расчет надежности программного обеспечения клиента
Надежность программного обеспечения клиента рассчитывается по формуле (4):
Р клиент = Р ОС Р ВБ , (4)
где Р ОС - надежность операционной системы, установленной на клиенте;
Р ВБ - надежность веб-браузера, используемого клиентом.
В качестве операционной системы, установленной на клиенте, используется Windows 7 Home Premium, компания производитель Microsoft Corporation установила вероятность безотказной работы равной:
Р ОС = 0,98.
Для пакета Internet Explorer 10, компания производитель установила вероятность безотказной работы равной:
Р ВБ = 0,9.
Вероятность безотказной работы программного обеспечения клиента составляет:
Р клиент = 0,98 0,9 = 0,88
Расчет надежности программного обеспечения
Надежность программного обеспечения целиком определяется ошибками разработки. Для среды, в которой по мере обнаружения ошибки исправляются и не вносятся в результаты новые ошибки, надежность программного обеспечения со временем увеличивается.
Используя модель Миллса, рассчитаем надежность программного обеспечения разработанной системы. В программу было искусственно занесено S = 25 ошибок и при Т = 100 запусков обнаружено V = 24 искусственных и n = 4 собственных ошибок. Предполагается, что все ошибки, как искусственные, так и собственные, имеют равную вероятность быть обнаруженными. Тогда первоначальное количество ошибок можно определить из соотношения (5):
Вероятность, с которой можно высказать такое предположение в случае, когда не обнаружены все искусственно рассеянные ошибки, рассчитывается по формуле (6):
где К? n - число собственных ошибок; числитель и знаменатель формулы являются биноминальными коэффициентами вида (7):
Получаем вероятность того, что в системе было 5 собственных ошибок С = 0,75.
Вероятность неверного исхода определяется по формуле 8.
Вероятность безотказной работы (ВБР) определяется формулой (9):

График зависимости безотказной работы программного обеспечения системы от времени (в часах) представлен на рисунке 23.

Рисунок 23 - Зависимость вероятности безотказной работы программного обеспечения от времени (в часах)
Надежность программной части. По формуле (5.2) определим вероятность безотказной работы всей программной части системы и построим график зависимости. График зависимости вероятности безотказной работы программной части системы от времени (в часах) представлен на рисунке 24.

Рисунок 24 - Зависимость вероятности безотказной работы программной части системы от времени (в часах)
По рисунку видно, что ошибки разработки программного обеспечения уменьшают надежность всей системы. По мере выявления и устранения ошибок разработки, их влияние на надежность системы уменьшается.
В данном изложении рассматриваются общие методы получения оценок параметров, определяющих надежность изделий.Эти методы могут быть использованы при обработке результатов наблюдений над изделием, срок безотказной работы которых подчинен тому или иному распределению - показательному, Вейбулла, логарифмически нормальному и др.
Чисто технически трудности заставляют нас ограничиться только планами и . Естественно, что последующие результаты применимы при обработке результатов не только элементов, но и сложных систем и машин (например, космических кораблей, комбайнов, сложной техники).
План
Напомним, что план означает испытание N элементов до отказа последнего элемента;отказавшие элементы не заменяются новыми.
План можно использовать или в случае, когда элементы сравнительно ненадежны, или же при проведении ускоренных испытаний.
Предположим, что испытываемые элементы занумерованы числами 1, …, N и i-й элемент отказывает в момент . Первый отказ наступает в момент , где - номер элемента, оказавшего первым; - случайное число. Второй отказ наступает в момент и т. д.
Наконец, в момент отказывает последний элемент.
В статистике так упорядоченную последовательность чисел ![]() называют вариационным рядом
или порядковыми статистиками для наблюдений .
называют вариационным рядом
или порядковыми статистиками для наблюдений .
При использовании наблюдаются только те отказы, которые происходят до момента времени Т. Если - последовательные моменты отказов, то, в результате испытаний мы наблюдаем случайное число отказов, происходящих в моменты ![]() (Отказ с номером , если он возможен, наступает после момента Т).
(Отказ с номером , если он возможен, наступает после момента Т).
Таким образом, означает номер последнего отказа, который происходит до момента Т окончания испытаний. Если элементы достаточно надежно работают в интервале времени (0, Т), то нередко случается, что отказы не наблюдаются и =0.
Заметим теперь же, что отсутствие отказов во время испытаний, т.е. условие =0, не дает нам право заключить, что надежность изделий равна 1.
Наиболее полной характеристикой надежности элементов является функция распределения F(t)
времени безотказной работы.
О виде функции распределения можно судить по так называемой эмпирической функции распределения, определяемой посредством равенства для значений х, .
Согласно теореме Гливенко с вероятностью 1 .

Рис.1. Эмпирические функции распределения и
.
На рисунке показаны эмпирические функции распределения и , когда теоретическая функция распределения . Если используется план , то значения эмпирической функции могут быть определены только для . Если же используется план , то значения эмпирической функции определяются только до уровня .
Оценкой плотности вероятностей может служить так называемая гистограмма .
В отличие от эмпирической функции гистограмма
может быть построена различными способами.
Например, можно разбить область значений времени t на интервалы и на каждом из этих интервалов положить
где - число отказов, которые наблюдались в интервале .

Рис.2. Гистограмма для показательного закона F(t)
На рис. 2, а приведен пример построения гистограммы для показательного закона
При втором способе выбирается число интервалов, так что , при этом , а остаток от деления также близок к Первый интервал - , где совпадает с моментом отказа, второй интервал - ![]() совпадает с моментом отказа и т.д., наконец, k
-й интервал -
совпадает с моментом отказа и т.д., наконец, k
-й интервал -
Последний, (k+1)-й, интервал -
На каждом из k интервалов группировки , полагаем

на интервале Гистограмма, построенная по этому способу для
Функция опасности отказов определяется по формуле ![]()
Если число испытываемых элементов N велико и интервалы между последовательными моментами отказов сравнительно невелики, то можно построить эмпирическую функцию опасности отказов. Ось времени разбиваем на несколько участков
Оценкой для является отношение - случайная величина. За оценку для берем  - число элементов, отказавших на интервале Эмпирическую функцию опасности отказов полагаем равной отношению
- число элементов, отказавших на интервале Эмпирическую функцию опасности отказов полагаем равной отношению  При этом интервалы можно выбирать способом, аналогичным одному из описанных выше способов построения гистограммы.
При этом интервалы можно выбирать способом, аналогичным одному из описанных выше способов построения гистограммы.
Иногда не обязательно знать всю функцию распределения , ее плотность или ее функцию отказов , а достаточно знать лишь некоторые характеристики: моменты, квартили и др.
Момент k - го порядка в случае плана определяется по формуле
![]()
центральный момент порядка - по формуле
![]()
Число такое, что , называется квантилью уровня р .
Эмпирической квантилью уровня р называется одно из решений уравнения . Мы всюду предполагаем, что является непрерывной.
Три типа статистической устойчивости
В случае плана нам известна вся эмпирическая функция распределения , а в случае плана - лишь часть ее определенная для значений .
Для оценки неизвестной функции распределения и различных числовых ее характеристик возможны три принципиально различных подхода, соответствующих различным реальным условиям, в которых решается задача.
В первом, наиболее простом случае заранее известен тип закона распределения .
Например, в результате теоретических исследований и последующей экспериментальной проверки показано, что для определенного типа элементов и аппаратуры закон распределения времени безотказной работы является показательным, т.е. ![]() Неизвестно лишь значение параметра которое надо оценить по результатам проведенных испытаний.
Неизвестно лишь значение параметра которое надо оценить по результатам проведенных испытаний.
Во втором случае не теоретических соображений, из которых следовало бы, что тип закона распределения должен быть вполне определенным, например, показательным, логарифмически нормальным или каким-то другим. Однако результаты испытаний показывают, что эмпирические функции распределения могут быть приближены плавно меняющимися функциями распределений.
Из предварительной обработки экспериментальных данных видно, что качественный характер поведения эмпирических функций распределения или гистограмм не меняется от партии к партии.
Пусть гистограммы имеют существенную асимметрию и одновершинны.
В таких случаях подбирают одно из возможных семейств функций распределения, или плотностей, для которого качественное поведение функций распределения, или плотностей, соответствует полученным экспериментальным данным.
Если семейство распределений выбрано, то задача определения функции и ее характеристик сводится к оценке по результатам испытания неизвестных значений параметров или функций от них.
Например, если мы пытаемся приближенно описать данные с помощью логарифмически нормального закона, то неизвестными значениями параметров являются
При этом в самом начале работ полезно сравнить результаты, получаемые при использовании двух-трех типов семейств распределений. Если два семейства дают одинаково хорошие результаты, то для дальнейшего использования выбирается то из них, для которого можно предложить теоретические обоснования.
В том же случае, когда теоретических предпосылок для выбора распределения нет, нужно предпочесть то, для которого трудоемкость числовых расчетов меньше.
Возможен, однако, и третий случай условий производства, когда качественный характер эмпирической функции меняется от партии к партии или же когда для приближений нужны семейства со многими неизвестными параметрами и соответственно требуются громоздкие вычисления необходимых характеристик.
В этих случаях можно использовать некоторые методы непараметрической статистики, т.е. методы, не связанные с аналитическим видом функции распределения .
Для весьма надежных элементов реализация плана или приводит к необходимости проведения испытаний в течение многих тысяч часов. Именно по этой причине часто используются различные планы с фиксированной длительностью испытаний (, , , и др.).
При этом по наблюдениям, полученным за ограниченный промежуток времени, нужно оценить различные показатели надежности, связанные с отказами, которые могут произойти после момента Т
, среднее время безотказной работы в течение времени и др.
Использование результатов за ограниченное время наблюдения для получения оценок всевозможных характеристик надежности законно в первом случае, когда вид функции распределения нам известен до опыта и только неизвестны значения параметров, определяющих этот закон.
Во втором случае надо иметь достаточный статистический материал, который хотя бы косвенно подтверждал правильность выводимых числовых оценок. Таким косвенным подтверждением могут служить результаты испытаний отдельных партий элементов, проводившихся в течение длительного времени, или сведений об отказах эксплуатируемого оборудования.
Наконец, в третьем случае, когда нет устойчивости даже качественного поведения эмпирической функции распределения, получения оценок любых характеристик надежности, которые определяются по значениям для t > T , где Т - время испытаний, не является законным. В этом случае, прежде всего, необходимо отладить технологический процесс.
В подтверждение этих соображений рассмотрим следующий пример. В нем мы намеренно "сгустили краски". Предположим, что проводятся испытания элементов N=100. Каждый элемент состоит из двух частей, отказ каждой из которых приводит к отказу элемента (например, проводящий слой сопротивления и контакты). Отказы обеих частей происходят независимо друг от друга.
Таким образом, если - момент, когда произойдет отказ первой части (обрыв), а - момент отказа второй части (уход параметра за пределы допуска), то считается, что отказ элемента произойдет в момент. Предположим далее, что

Однако экспериментатору неизвестно, что закон распределения времени безотказной работы
Вид функции показан на рис. 3.

Рис.3. График функции F(t)
Было решено проводить испытания в течение Т=500 час. Вероятность отказа первого элемента равна
![]()
Таким образом, мы в среднем наблюдаем число отказов NF(T)
приблизительно равным 100, причем практически все наблюдаемые отказы будут только первого типа (обрыв), так как отказы второго типа (уход параметров) при сделанных выше предположениях начнут наступать после 800 час работы, но зато уже к 1200 час работы почти все элементы выйдут из строя вследствие отказов второго типа.
Отказов второго типа в течение Т=500 час мы не наблюдаем, поэтому ошибочно считаем, что закон , и по результатам этих испытаний пользуясь методами следующего параграфа, находим оценку для близкую к 2000.
Итак, по результатам испытаний, проводимых в течение Т=500 час, сделан ошибочный вывод относительно характера распределения.
Вывод из этого примера таков. Надо сначала проверить теоретически или экспериментально (а лучше обоими путями), что вид закона и при значениях t , больших времени Т проведения испытаний, не меняется, а уже затем получать оценки для характеристик надежности.
Рассмотрим теперь некоторые общие методы получения оценок параметров распределения времени безотказной работы. При оценке параметров конкретного семейства распределений могут быть употреблены различные методы. В зависимости от используемого метода будут получаться отличающиеся друг от друга оценки неизвестных значений параметров.
Необходимо провести сравнение различных методов и для дальнейшего выбрать метод, дающий наилучшие результаты. В тех случаях, когда вычисления приходится выполнять вручную, нужно оценивать метод и с точки зрения трудоемкости вычислений.
Графические методы
Первая и наиболее простая группа методов - графические методы оценки. Они применимы для некоторых семейств , содержащих два неизвестных параметра График функции распределения можно представить в виде совокупности точек (t, p) на плоскости, где ![]() . Основная идея графического метода состоит в том, что подбирается такая непрерывная замена координат
. Основная идея графического метода состоит в том, что подбирается такая непрерывная замена координат ![]() , что при этом график функции распределения , где
, что при этом график функции распределения , где ![]() , становится прямой линией . Если такую замену переменных удалось отыскать, то на плоскости любая функция распределения этого семейства будет представима в виде прямой или, что то же самое, в виде прямой
, становится прямой линией . Если такую замену переменных удалось отыскать, то на плоскости любая функция распределения этого семейства будет представима в виде прямой или, что то же самое, в виде прямой
Используем этот факт для оценки параметров Предположим, что в результате испытаний получены N
значений некоторой случайной величины (например, времени безотказной работы элемента или интервалов между отказами в аппаратуре).
По этим значениям мы можем построить эмпирическую функцию распределения . Так как эмпирическая функция при больших N
лежит вблизи от теоретической функции распределения , то после замены переменных график ![]() , а
, а ![]() , будет лежать в непосредственной близости от графика , являющегося прямой вида (1).
, будет лежать в непосредственной близости от графика , являющегося прямой вида (1).
Оценив с помощью линейки тангенс наклона k и свободный член b и приравняв их теоретическим значениям, получаем уравнения
из которых находим оценки неизвестных значений параметров
Уместно заметить, что графический метод применим для любого плана , , , , , .
Например, в случае плана по результатам испытаний можем построить только часть для значений - число элементов, отказавших за время проведения испытаний. Если к полученному куску эмпирической функции распределения применить преобразования , то на плоскости получим кусок ломаной, близкой к одной из прямых вида (1).). По этому куску оцениванием k и b и снова приходим к уравнению (2).
Для примера, рассмотрим три семейства распределений. В случае нормального семейства распределений.
в качестве преобразования рассмотрим функцию , обратную к функции . При этом получаем
Таким образом, (3) соответствует (2), когда
Для удобства пользования выпускается специальная нормальная вероятностная бумага. По оси абсцисс отложены значения t случайной величины, а по оси ординат - значения функции . При этом ось t проводится через точку 0, соответствующую .
Около каждого значения отмечается соответствующее ему значение р (рис. 4).

Рис.4. Нормальная вероятностная бумага
Функция распределения записывается в виде прямой y=x . Прямой соответствует функция распределения нормальной случайной величины со средним и дисперсией .
Таким образом, с помощью вероятностной бумаги можно легко проверять "на глаз" нормальность закона распределения, а заодно и оценивать его параметры. Если ломаная имеет заметную искривленность, то это говорит о том, что истинный закон распределения не является нормальным.
Если же искривленности нет, то, проводя "на глаз" прямую, наиболее плотно прилегающую к ломаной, легко находим оценки для и . равно абсциссе точки А, где А - точка пересечения прямой с осью t; равно расстоянию от А до В, где В - точка на оси t, в которой величина перпендикуляра, опущенного из точки прямой на ось t, равна 1 (в единицах масштаба оси абсцисс).
В случаях логарифмически нормального закона ![]() , поэтому
, поэтому
Если задано семейство показательных распределений со сдвигом
 (4)
(4)
где . Поэтому в качестве выбираем функцию  . Сравнивая (4) с (1), видим, что .
. Сравнивая (4) с (1), видим, что .
Наконец, если нам задано семейство распределений Вейбулла
![]() то
то
 (5)
(5)
Сравнивая (5) с (1), находим, что

Вид бумаги для закона Вейбулла показан на рис. 5.

Рис.5. Вид бумаги для закона Вейбулла
Таким образом, тангенс угла наклона равен р, а логарифм равен величине отрезка ОА, отсекаемого прямой на оси ординат.
Методы квантилей и моментов
Для получения оценок неизвестных значений параметров, определяющих вид закона распределения времени безотказной работы, могут быть использованы методы моментов и квантилей.
Здесь мы рассматриваем эти методы с точки зрения обработки результатов испытаний, полученных при использовании некоторых планов типа Б. Для определенности мы ограничимся случаем двух неизвестных параметров и .
Пусть закон распределения времени безотказной работы имеет непрерывно дифференцируемую плотность, принимающую положительные значения для любых возможных значений параметров , .
Если испытания проводились по плану , , то момент появления -го отказа можно рассматривать как эмпирическую квантиль, соответствующую уровню ![]() . Если и N достаточно велики, то можно считать, что имеют нормальное распределение с нулевым средним и матрицей дисперсий
. Если и N достаточно велики, то можно считать, что имеют нормальное распределение с нулевым средним и матрицей дисперсий

где 
Если бы значения квантилей , были ним известны точно, то значения параметров , можно было бы найти из уравнений (6)
Нам известны, лишь приближенные значения этих квантилей - моменты появления l -го и r -го отказов. Заменяя в уравнениях (6) значения квантилей их оценками, получаем уравнения
решения которых являются состоятельными оценками для параметров , при ![]() , что непосредственно следует из непрерывности функции . Можно показать, что эти оценки при весьма общих предположениях типа гладкости функции являются асимптотически несмещенными и асимптотически нормально распределенными.
, что непосредственно следует из непрерывности функции . Можно показать, что эти оценки при весьма общих предположениях типа гладкости функции являются асимптотически несмещенными и асимптотически нормально распределенными.
Поэтому наиболее существенными показателями качества таких оценок являются их дисперсии.
Проиллюстрируем метод квантилей на примере закона Вейбулла
![]() Испытания проводятся по плану . Выбирается значение l
(можно выбрать ). В результате испытаний фиксируются значения и моментов l
-го и r
-го отказов.
Испытания проводятся по плану . Выбирается значение l
(можно выбрать ). В результате испытаний фиксируются значения и моментов l
-го и r
-го отказов.
Уравнения (7) переписываются в виде

Решая их относительно неизвестных значений параметров p, , получаем оценки

Если предположить, что у существуют вторые непрерывные частные производные по t и параметрам , , то, используя обычный прием разложения в ряд Тейлора, можно получить приближенное выражение для дисперсии оценок параметров , .
Введем обозначения
Из уравнений (7) находим 
Заметив, что ![]() , получаем с точностью до бесконечно малых высших порядков
, получаем с точностью до бесконечно малых высших порядков
 (8)
(8)
Аналогично находим, что
(8")
Разрешая эти линейные уравнения (8) и (8") относительно ошибок , получаем их в виде линейных комбинаций от :
Отсюда, используя матрицу вторых моментов для квантилей , можно найти дисперсии ошибок
 (9)
(9)
В частности, в случае закона Вейбулла получаем

Метод квантилей в несколько видоизмененной форме можно использовать и в случае планов . В этом случае вместо уравнения (6) можем записать
где . Однако значения при ![]() нам неизвестны. Нам известны лишь числа
нам неизвестны. Нам известны лишь числа ![]() отказов, происшедших к моментам . При больших значениях N отношения
отказов, происшедших к моментам . При больших значениях N отношения ![]() близки к теоретическим значениям . Поэтому, заменяя в (10) значения их оценками, получаем уравнения
близки к теоретическим значениям . Поэтому, заменяя в (10) значения их оценками, получаем уравнения
 (11)
(11)
для нахождения оценок . Используя разложение функции в ряд Тейлора
по параметрам и , можно найти приближенные выражения для дисперсий оценок.
Если объем выборки N велик, то можно для получения оценки параметров использовать не все данные, а только значения k определенным образом выбранных эмпирических квантилей,
При этом числа подбираются таким образом, чтобы дисперсии ошибок неизвестных параметров были бы минимальными.
Например, для случая закона экспоненциального типа оценка ищется в виде линейной комбинации
 (12)
(12)
где коэффициенты и числа подобраны таким образом, чтобы дисперсия оценки была наименьшей. Как известно, наилучшей оценкой для параметра при использовании всех данных является . Подсчет отношения дисперсий этих оценок в зависимости от выбранного числа квантилей k показал, что
Так же как и метод квантилей, метод моментов может быть использован только при обработке результатов испытаний, в которых наблюдаемое число отказов достаточно велико. Если испытания проводится в соответствии с планом , то условная плотность вероятности распределения момента отказа при условии, что такой отказ произошел за время испытаний Т, равна .
Таким образом, для момента k-го порядка, относящегося к наблюдаемым отказам, имеем  (13)
(13)