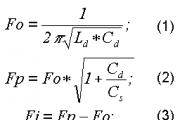Центр дуги сопряжения должен быть равноудален (находится на одинаковом расстоянии) от каждой из двух сопрягаемых (данных) прямых. Любая из точек сопряжения (точки входа) представляет собой пересечение перпендикуляра, опущенного из центра сопряжения на соответствующую прямую.

Алгоритм построения сопряжения двух прямых дугой заданного радиуса (рис. 13.39, а, б) следующий:

1. На расстоянии (R ), равном радиусу дуги сопряжения, проводятся две прямые, параллельные сопрягаемым прямым.

2. Определяют их точку пересечения, являющуюся центром сопряжения (О ).

3. Из точки (О ) проводят перпендикуляры к заданным прямым и находят точки сопряжения (А ) и (В ).

4. Из точки (А ) к точке (В ) строят дугу сопряжения заданного радиуса (R ).

Рисунок 13.49

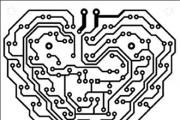
Типичными примерами сопряжений являются контуры деталей, изображенных на рис. 13.40.

В AutoCAD сопряжение двух отрезков прямых (рис. ХХ а) выполняется командой «Сопрячь» (Скругление, Шпонка, Fillet) из меню «Модификация». После выбора команды следует параметром «Radius» задать радиус сопряжения (например, 10 мм), затем последовательно указателем мышки отметить оба отрезка (см. рис. ХХ б).

Current settings: Mode = TRIM, Radius = 5.0000

radius

Specify fillet radius <5.0000>: 10

Select first object or :

Select second object:

Полученный элемент состоит из двух исходных отрезков и дуги сопряжения R=10мм (см. рис. ХХ в).

Рис. ХХ а) Рис. ХХ б) Рис. ХХ в)

1.2. Сопряжение дуги окружности радиуса R и прямой а с дугой заданного радиуса R1

Для выполнения этого сопряжения (рис. 3.31) сначала определяют множество центров дуг радиуса R 1 . Для этого на расстоянии R 1 от прямой а проводят параллельную ей прямую m , а из центра О радиусом (R + R 1 ) – дуги концентрической окружности. Точка О 1 будет центром дуги сопряжения. Точка сопряжения С получена на перпендикуляре, опущенном из точки О 1 на прямую а , а точка В – на прямой, соединяющей точки О и О 1 .

Рисунок 3.31

На рис. 3.32 представлен пример изображения контура подшипника, в построении которого использован рассмотренный вид сопряжений.

Рисунок 3.32

Сопряжение прямой и окружности в AutoCAD имеет смысл при построении к окружности отрезка прямой, являющейся касательной к этой окружности. Для этого при построении отрезка начальную точку отрезка задают по координатам или объектной привязкой, конечную точку задают привязкой «Касательная» (Прыжок в тангенс) относительно окружности (работа с привязкой описана в приложении ХХХХХХХХХХХ).

1.3. Сопряжение дуг двух окружностей с радиусами R1 и R2 , дугой сопряжения радиуса R

Различают внешнее (рис. 13.42,а), внутреннее (рис. 13.42, б) и смешанное (рис. 13.42, в) сопряжения. В первом случае центр сопряжения является точкой пересечения дуги окружностей радиусов R 1 +R и R 2 +R, во втором - на пересечении окружностей радиусов R-R 1 и R-R 2 , в третьем - на пересечении дуг окружностей радиусов R+R 1 и R-R 2 . Точки сопряжения А 1 и А 2 лежат на прямых, соединяющих центр сопряжения с центром соответствующей окружности.

Рассмотрим случай внешнего сопряжения двух окружностей в AutoCAD. На рис. ХХ.а показаны две опорные окружности с радиусами R 1 и R 2 , центры которых лежат на концах пунктирной линии. Из центра окружности R 1 строят вспомогательную окружность с радиусом R 1 +R, а из центра окружности R 2 – окружность R 2 +R как это показано на рис. ХХ.б (вспомогательные окружности показаны штриховой линией). Затем из точки пересечения вспомогательных окружностей строят окружность с радиусом R (на рис. ХХ в показана штрих-пунктирной линией). Окончательные построения выполняют с помощью команды «Обрезать» из меню «Модификация». В качестве секущих объектов выбирают опорные окружности и обрезают верхнюю часть окружности R, затем удаляют вспомогательные окружности (результат построения показан на рис. ХХ.г).

Рисунок ХХ.а Рисунок ХХ.б

Рисунок ХХ.в Рисунок ХХ.г

Теперь рассмотрим случай внутреннего сопряжения двух окружностей в AutoCAD. Аналогично предыдущему случаю строят опорные окружности с радиусами R 1 и R 2 . Из центра окружности R 1 строят вспомогательную окружность с радиусом R–R 1 , а из центра окружности R 2 – окружность R–R 2 . Затем из точки пересечения вспомогательных окружностей строят окружность с радиусом R (см. рис. ХХХ.а). Лишние элементы удаляют аналогично предыдущему случаю (результат показан на рис. ХХХ.б).

Цель работы: изучить выполнение сопряжений кривых, выполнить чертеж детали с сопряжениями

1. Деление окружностей на равные части

Деление окружности 4 и 8 равных частей

1) Два взаимных перпендикуляра диаметра окружности делят ее на 4 равные части (точки 1, 3, 5, 7).

Деление окружности на 3, 6, 12 равных частей

1) Для нахождение точек, делящих окружность радиуса R на 3 равные части, достаточно из любой точки окружности, например точки А(1), провести дугу радиусом R.(т.2,3) (рисунок 1 б).

2) Описываем дуги R из точек 1 и 4 (рисунок 1 в).

3) Описываем дуги 4 раза из точек 1, 4, 7, 10 (рисунок 1 г).

Рисунок 1 – Деление окружностей на равные части

а – на 8 частей; б – на 3 части; в – на 6 частей;

г – на 12 частей; д – на 5 частей; е – на 7 частей.

Деление окружности на 5, 7, равных частей

1) Из точки А радиусом R проводят дугу, которая пересекает окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку С. Из точки С радиусом R 1 =С1, проводят дугу, которая пересекает горизонтальную осевую линию в точке m. Из точки 1 радиусом R 2 =1m, проводят дугу, пересекающую окружность в точке 2. Дуга 12=1/5 длины окружности. Точки 3,4,5 находят, откладывая циркулем отрезки, равные m1 (рисунок 1 д).

2) Из точки А проводим вспомогательную дугу радиусом R, которая пересекает окружность в точке n. Из нее опускаем перпендикуляр на горизонтальную осевую линию. Из точки 1 радиусом R=nc, делают по окружности 7 засечек и получают 7 искомых точек (рисунок 1 е).

2. Построение сопряжений

Сопряжением называется плавный переход одной линии в другую.

Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях:

1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восстановленном из точки сопряжения (рисунок 2 а).

2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения (рисунок 2 б).

Рисунок 2 – Положения о сопряжениях

а – для прямой и дуги; б – для двух дуг.

Сопряжение двух сторон угла дугой окружности и заданного радиуса

Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса выполняют следующим образом:

Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии (рисунок 3 а, б). Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые - стороны угла. Дугу заканчивают в точках сопряжения n и n 1 , которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла. При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (рисунок 3 в). Из вершины угла А проводят дугу радиусом R, равным радиусу сопряжения. На сторонах угла получают точки сопряжения n и n 1 . Из этих точек, как из центров, проводят дуги радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения. Из центра О описывают дугу сопряжения.

Глава 3. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

§ 14. Общие сведения

При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи - деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений прямых с дугами окружностей и дуг окружностей между собой. Сопряжением называют плавный переход дуги окружности в прямую или в дугу другой окружности.

Наиболее часто встречаются задачи на построение следующих сопряжений: двух прямых дугой окружности (скруглением углов); двух дуг окружностей прямой линией; двух дуг окружностей третьей дугой; дуги и прямой второй дугой.

Построение сопряжений связано с графическим определением центров и точек сопряжения. При построении сопряжения широко используются геометрические места точек (прямые, касательные к окружности; окружности, касательные друг к другу). Это объясняется тем, что они основаны на положениях и теоремах геометрии.

10. Вопросы для самопроверки

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

15. Какая плоская кривая называется эвольвентой?

15. Деление отрезка прямой

§ 15. Деление отрезка прямой

Чтобы разделить заданный отрезок АВ на две равные части, точки его начала и конца принимают за центры, из которых проводят дуги радиусом, по величине превышающим половину отрезка АВ. Дуги проводят до взаимного пересечения, где получают точки С и D. Линия, соединяющая эти точки, разделит отрезок в точке К на две равные части (рис. 30, а).

Чтобы разделить отрезок АВ на заданное количество равных участков п, под любым острым углом к АВ проводят вспомогательную прямую, на которой из общей заданной прямой точки откладывают п равных участков произвольной длины (рис. 30, б). Из последней точки (на чертеже - шестой) проводят прямую до точки В и через точки 5, 4, 3, 2, 1 проводят прямые, параллельные отрезку 6В. Эти прямые и отсекут на отрезке АВ заданное число равных отрезков (в данном случае 6).

Рис. 30 Деление заданного отрезка АВ на две равные части

Изображение:

16. Деление окружности

§ 16. Деление окружности

Чтобы разделить окружность на четыре равные части, проводят два взаимно перпендикулярных диаметра: на пересечении их с окружностью получаем точки, разделяющие окружность на четыре равные части (рис. 31, а).

Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 31, б).

На двенадцать равных частей окружность делят следующим образом. Делят окружность на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 31, в).

Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7 равных участков.

Рис. 31 Пользуясь радиусом, нетрудно разделить окружность и на несколько равных участков.

Изображение:

17. Округление углов

§ 17. Скругление углов

Сопряжение двух пересекающихся прямых дугой заданного радиуса называют скруглением углов. Его выполняют следующим образом (рис. 32). Параллельно сторонам угла, образованного данными

прямыми, проводят вспомогательные прямые на расстоянии, равном радиусу. Точка пересечения вспомогательных прямых является центром дуги сопряжения.

Из полученного центра О опускают перпендикуляры к сторонам данного угла и на пересечении их получают точки сопряжения А а В. Между этими точками проводят сопрягающую дугу радиусом R из центра О.

Рис. 32 Сопряжение двух пересекающихся прямых дугой заданного радиуса называют скруглением углов

Изображение:

18. Сопряжение дуг окружностей прямой линией

§ 18. Сопряжение дуг окружностей прямой линией

При построении сопряжения дуг окружностей прямой линией можно рассмотреть две задачи: сопрягаемая прямая имеет внешнее или внутреннее касание. В первой задаче (рис. 33, а) из центра дуги

меньшего радиуса R1 проводят касательную вспомогательной окружности, проведенной радиусом R - RI. Ее точку касания Ко используют для построения точки сопряжения А на дуге радиуса R.

Для получения второй точки сопряжения А 1 на дуге радиуса R 1 проводят вспомогательную линию О 1 А 1 параллельно О А. Точками A и А 1 будет ограничен участок внешней касательной прямой.

Задача построения внутренней касательной прямой (рис. 33, б) решается, если вспомогательную окружность построить радиусом, равным R + R 1 ,

Рис. 33 Сопряжение дуг окружностей прямой линией

Изображение:

19. Сопряжение двух дуг окружностей третьей дугой

§ 19. Сопряжение двух дуг окружностей третьей дугой

При построении сопряжения двух дуг окружностей третьей дугой заданного радиуса можно рассмотреть три случая: когда сопрягающая дуга радиуса R касается заданных дуг радиусов R 1 и R 2 с внешней стороны (рис. 34, а); когда она создает внутреннее касание (рис. 34, б); когда сочетаются внутреннее и внешнее касания (рис. 34, в).

Построение центра О сопрягающей дуги радиуса R при внешнем касании осуществляется в следующем порядке: из центра О 1 радиусом, равным R + R 1 , проводят вспомогательную дугу, а из центра O 2 проводят вспомогательную дугу радиусом R + R 2 . На пересечении дуг получают центр О сопрягаемой дуги радиуса R, а на пересечении радиусом R + R 1 и R + R 2 с дугами окружностей получают точки сопряжения А и А 1 .

Построение центра О при внутреннем касании отличается тем, что из центра О 1 R - R 1 а из центра О 2 радиусом R - R 2 . При сочетании внутреннего и внешнего касания из центра О 1 проводят вспомогательную окружность радиусом, равным R - R 1 , а из центра О 2 - радиусом, равным R + R 2 .

20. Сопряжение дуги окружности и прямой линии второй дугой

§ 20. Сопряжение дуги окружности и прямой линии второй дугой

Здесь может быть рассмотрено два случая: внешнее сопряжение (рис. 35, а) и внутреннее (рис. 35, б). В том и в другом случае при построении сопрягающей дуги радиуса R центр сопряжения О лежит на пересечении геометрических мест точек, равно удаленных от прямой и дуги радиуса R на величину R 1 .

При построении внешнего сопряжения параллельно заданной прямой на расстоянии R 1 в сторону окружности проводят вспомогательную прямую, а из центра О радиусом,равным R + R 1 , - вспомогательную окружность, и на их пересечении получают точку О 1 - центр сопрягающей окружности. Из этого центра радиусом R проводят сопрягающую дугу между точками А и А 1 , построение которых видно из чертежа.

Построение внутреннего сопряжения отличается тем, что из центра О проводят вспомогательную дугу радиусом, равным R - R 1 .

Рис 34 Внешнее сопряжение дуги окружности и прямой линии второй дугой

Изображение:

Рис 35 Внутреннее сопряжение дуги окружности и прямой линии второй дугой

Изображение:

21. Овалы

§21. Овалы

Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами. Овалы состоят из двух опорных окружностей с внутренними сопряжениями между ними.

Различают овалы трехцентровые и многоцентровые. При вычерчивании многих деталей, например кулачков, фланцев, крышек и других, контуры их очерчивают овалами. Рассмотрим пример построения овала по заданным осям. Пусть для четырехцентрового овала, очерченного двумя опорными дугами радиуса R и двумя сопрягающими дугами радиуса r , заданы большая ось АВ и малая ось CD. Величину радиусов R u r надо определить путем построений (рис. 36). Соединим концы большой и малой оси отрезком AС, на котором отложим разность СЕ большой и малой полуосей овала. Проведем перпендикуляр к середине отрезка AF, который пересечет большую и малую оси овала в точках О 1 и О 2 . Эти точки будут центрами сопрягающихся дуг овала, а точка сопряжения будет лежать на самом перпендикуляре.

Рис. 36 Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами

22. Лекальные кривые

§ 22. Лекальные кривые

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.

Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее

Рис. 37

точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности - прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи. В пересечении одноименных лучей получают точки эллипса.

Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки - фокуса и от данной прямой - директрисы.

Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и ну-

меруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.

Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

Урок № 23.

Сопряжения

Показать несколько деталей, имеющих скругления.

Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе.

На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением.

При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т.е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания .

Задачи на сопряжения условно можно разделить на 3 группы.

Первая группа задач включает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построим окружность, касательную к прямой.

Построение окружности, касательной к прямой , связано с нахождением точки касания и центра окружности.

Задана горизонтальная прямая АВ , требуется построить окружность радиусом R , касательную к данной прямой (рис. 1).

Точка касания выбирается произвольно.

Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (О 1 , О 2 и т.д.) будут находиться на одинаковом расстоянии от заданной прямой, т.е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 1). Назовем эту линию линией центров .

Проведем линию центров параллельно прямой АВ на расстоянии R . Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например, точку О.

Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ . В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

Запишите в свои тетради в клетку следующие правила:

Если в сопряжении участвует прямая линия, то:

1)

центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

2) точка касания лежит на перпендикуляре, проведенном из центра окружности к заданной прямой.

Сопряжение двух прямых.

На плоскости две прямые могут располагаться параллельно или под углом друг к другу.

Чтобы построить сопряжение двух прямых, необходимо провести окружность, касательную к этим двум прямым.

Откройте рабочие тетради на странице 31.

Рассмотрим сопряжение двух непараллельных прямых.

Две непараллельные прямые располагаются друг к другу под углом, который может быть прямым, тупым или острым. При выполнении чертежей деталей часто такие углы необходимо скруглить дугой заданного радиуса (рис.1). Скругление углов на чертеже есть не что иное, как сопряжение двух непараллельных прямых дугой окружности заданного радиуса. Для выполнения сопряжения необходимо найти центр дуги сопряжения и точки сопряжения.

Известно, что если в сопряжении участвует прямая линия, то центр дуги сопряжения находится на линии центров, которая проводится параллельно заданной прямой на расстоянии, равном радиусу R дуги сопряжения.

Поскольку угол образован двумя прямыми, то проводят две линии центров параллельно каждой прямой на расстоянии, равном радиусу R дуги сопряжения. Точка их пересечения будет центром дуги сопряжения.

Для нахождения точек сопряжения из точки О опускают перпендикуляры на заданные прямые и получают точки сопряжения К и К 1 . Зная точки и центр сопряжения, из точки О радиусом R проводят дугу сопряжения. При обводке чертежа следует сначала обвести дугу, а затем касательные прямые.

При построении сопряжения прямого угла упрощается проведение линии центров, так как стороны угла взаимно перпендикулярны. От вершины угла откладывают отрезки, равные радиусу R дуги сопряжения, и через полученные точки К и К 1 , которые будут точками касания, проводят две линии центров, параллельные сторонам угла. Они будут являться одновременно и линиями центров, и перпендикулярами, определяющими точки сопряжения К и К 1 (стр. 31, рис.1).

Стр. 31, задание 4. Сопряжение двух параллельных прямых.

Чтобы построить сопряжение двух параллельных прямых, необходимо провести дугу окружности, касательной к этим прямым (рис.3).

Рис.3

Радиус этой окружности будет равен половине расстояния между заданными прямыми. Так как точка касания не задана, подобных окружностей можно провести множество. Центры их будут находиться на прямой, проведенной параллельно заданным прямым на расстоянии, равном половине расстояния между ними. Эта прямая будет линией центров.

Точки касания (К 1 и К 2 ) лежат на перпендикуляре, опущенном из центра касательной окружности на заданные прямые (рис. 3а). Так как центр касательной окружности не задан, перпендикуляр проводится произвольно. Отрезок КК 1 делят пополам (рис.3б), проводят через точки пересечения засечек прямую линию параллельно заданным прямым, на которой будут располагаться центры окружностей, касательных к заданным параллельным прямым, т.е. эта линия будет линией центров. Поставив ножку циркуля в точку О , проводят дугу сопряжения (рис. 3в) от точки К до точки К 1 .

Построение прямых, касательных к окружностям

(Р.Т. стр.33).

Задание 1 . Проведите прямую, касательную к окружности через точку А , лежащую на окружности.

Из точки О проводим прямую OB через точку А . Из точки А любым радиусом проводим окружность. При пересечении с прямой получили точки 1 и 2. Из этих точек любым радиусом проводим дуги до пересечения между собой в точках C и D . Из точки C или D проводим прямую через точку А .

Она и будет касательной к окружности, так как касательная всегда перпендикулярна радиусу, проведенному в точку касания.

Задание 2 .

Это построение аналогично построению перпендикуляра к прямой через заданную точку, которое можно выполнить с помощью двух угольников.

Сначала угольник 1 кладется так, чтобы его гипотенуза совпадала с точками O и A . Затем к угольнику 1 прикладывается угольник 2 , который будет направляющим, т.е. по которому будет сдвигаться угольник 1 . Потом угольник 1 приставляем другим катетом к угольнику 2. Затем катаем угольник 1 по угольнику 2 до тех пор, пока гипотенуза не совпадет с точкой A . И проводим прямую, касательную к окружности через точку A .

Задание 3 . Проведите прямую, касательную к окружности через точку, не лежащую на этой окружности.

Даны окружность радиусом R и точка А , не лежащая на окружности, требуется провести из точки А прямую, касательную к данной окружности в верхней ее части. Для этого необходимо найти точку касания. Мы знаем, что точка касания лежит на перпендикуляре, проведенном из центра окружности к касательной прямой. Следовательно, касательная и перпендикуляр образуют прямой угол.

Зная, что всякий угол, вписанный в окружность и опирающийся на ее диаметр, является прямым, соединив точки А и О , принимают отрезок АО за диаметр описанной окружности. В пересечении описанной окружности и окружности радиуса R будет находиться вершина прямого угла (точка К ). Отрезок АО делим пополам при помощи циркуля, получаем точку О 1 (рис.4, б).

Из центра О 1 радиусом, равным отрезку АО 1 , проводим окружность, получаем точки К и К 1 в пересечении с окружностью радиуса R (рис.4 ,в).

Так как нужно провести только одну касательную к верхней части окружности, выбирают нужную точку касания. Этой точкой будет точка К . Точку К соединяем с точками А и О , получаем прямой угол, который опирается на диаметр АО описанной окружности радиусом R 1 . Точка К – вершина этого угла (рис.4, г), отрезки ОК и АК – стороны прямого угла, следовательно, точка К будет искомой точкой касания, а прямая АК – искомой касательной.

Рис.4

Проведение прямой, касательной к двум окружностям.

Даны две окружности радиусами R и R 1 , требуется построить касательную к ним. Возможны два случая касания: внешнее и внутреннее.

При внешнем касании касательная прямая находится с одной стороны от окружностей и не пересекает отрезок, соединяющий центры данных окружностей.

При внутреннем касании касательная прямая находится с разных сторон от окружностей и пересекает отрезок, соединяющий центры окружностей.

Стр. 33. Задание 5 . Проведите прямую, касательную к двум окружностям. Касание внешнее.

Прежде всего необходимо найти точки касания. Известно, что они должны лежать на перпендикулярах, проведенных из центров окружностей (О и О 1 ) к касательной.

Из точки О проводим окружность радиусом R - R 1 ,так как касание внешнее.

Разделим расстояние ОО 1 пополам и проведем окружность радиусом R =ОО 2 =О 1 О 2

Эта окружность пересекает окружность с радиусом R - R 1 в точке К. Соединяем эту точку с О 1 .

Из точки О через точку К проводим прямую до пересечения с окружностью радиусом R . Получили точку К 1 – первую точку касания.

Из точки О 1 проводим прямую, параллельную КК 1 , до пересечения с окружностью радиусом R 1 . Получили вторую точку касания К 2 . Соединяем точки К 1 и К 2 . Это и есть касательная к двум окружностям.

Задание 6 . Проведите прямую, касательную к двум окружностям. Касание внутреннее.

Построение аналогичное, только при внутреннем касании радиус вспомогательной окружности, проводящейся из точки О равен сумме радиусов окружностей R + R 1 .

Вторая группа задач на сопряжения включает в себя задачи, в которых участвуют только окружности и дуги. Плавный переход одной окружности в другую может происходить или непосредственно касанием, или через третий элемент – дугу окружности.

Касание двух окружностей может быть внешним (РТ: стр.32, рис.3) или внутренним (РТ: стр.32, рис.4).

Задание 3 (стр. 32)

При внешнем касании двух окружностей расстояние между центрами этих окружностей будет равно сумме их радиусов.

Из точки О радиусом R + R C проведем дугу. Из точки О 1 радиусом R 1 + R C О С - центр сопряжения.

Соединяем точки О и О 1 с центром сопряжения О С . На окружностях получили точки касания (сопряжения).

Из точки О С радиусом сопряжения R C 30 соединяем точки касания.

Задание 4 (стр. 32)

При внутреннем касании двух окружностей одна из касательных окружностей находится внутри другой окружности, и расстояние между центрами этих окружностей будет равно разности их радиусов.

Из точки О радиусом (R C – R ) проведем дугу. Из точки О 1 радиусом (R C – R 1 ) проведем дугу до пересечения с первой дугой. Получили точку О С - центр сопряжения.

Центр сопряжения О С соединяем с точками О и О 1 с и продлеваем прямую дальше.

На окружностях получили точки касания (сопряжения).

Из точки О С радиусом сопряжения R C 60 соединяем точки касания.

Третья группа задач на сопряжения включает в себя задачи на сопряжения прямой и дуги окружности дугой заданного радиуса.

Выполняя такое задание, решают как бы две задачи: проведение касательной дуги к прямой и касательной дуги к окружности. Касание в этом случае может быть как внешним, так и внутренним.

РТ: стр. 32. Задание 1. Сопряжение окружности и прямой. Касание внешнее. R C 20 .

Заданы прямая и окружность радиусом R , требуется построить сопряжение дугой радиуса R C 20 .

Так как в сопряжении участвует прямая линия, то центр дуги сопряжения находится на прямой, проведенной параллельно заданной прямой на расстоянии, равном радиусу сопряжения R C 20 . Поэтому параллельно заданной прямой на расстоянии 20 мм проводим еще одну прямую.

А центр дуги сопряжения при внешнем касании двух окружностей находится на окружности радиуса, равного сумме радиусов R и R C . Поэтому из точки О радиусом (R + R C О С

Затем находим точки касания. Первая точка касания - это перпендикуляр, опущенный из центра сопряжения на заданную прямую. Вторую точку сопряжения находим, соединив центр сопряжения О С и центр окружности R . Точка касания будет лежат на первом пересечении с окружностью, так как касание внешнее.

Затем из точки О С радиусом R C 20 соединяем точки сопряжения.

РТ: стр. 32. Задание 2. Сопряжение окружности и прямой. Касание внутреннее. R C 60 .

Параллельно заданной прямой проводим линию центров на расстоянии 60 мм. Из точки О радиусом (R с - R ) проводим дугу до пересечения с новой прямой (линией центров). Получим точку О С , которая является центром сопряжения.

Из О С проводим прямую через центр окружности точку О и перпендикуляр на заданную прямую. Получаем две точки касания. И затем из центра сопряжения радиусом 60 мм соединяем точки касания.

      Для грамотного и уверенного построения чертежей и изготовления графических дизайнерских работ, дизайнеру следует знать основные законы геометрических построений. Приводимые ниже примеры легко освоить на практике, применяя для построений циркуль и линейку или (на компьютере) любой векторный графический редактор.
Деление угла пополам
Из вершины А данного угла, как из центра провести дугу произвольного радиуса R, которая пересечет стороны угла в точках C,B (Шаг 1).
Из точки B, как из центра тем же радиусом R провести дугу (Шаг 2).

Из точки С, как из центра тем же радиусом R провести дугу до пересечения в точке D (Шаг 3).
Прямая, соединяющая точки A и D - искомая биссектриса (Шаг 4).

Деление прямого угла на 3 равные части
Из вершины прямого угла А, как из центра, следует провести дугу BC, произвольного радиуса R (Шаг 1).
Из точки B, как из центра, провести дугу, тем же радиусом R, до пересечения с дугой BC в точке D (Шаг 2).

Из точки C, как из центра, провести дугу, тем же радиусом R, до пересечения с дугой BC в точке E (Шаг 3).
Из точки А провести линии AD и AE (Шаг 4), которые и делят прямой угол BAC на три равных между собой угла BAE, EAD и DAC. Деление дуги окружности пополам
Из концов дуги АВ следует провести дуги радиусом R большим либо равным 1/2 длинны хорды АВ, которые пересекаются в точках M и N (Шаг 1).
Прямая, проведенная через точки M и N делит дугу и ее хорду АВ пополам и проходит через ее центр О (Шаг 2).
Деление окружностей. Построение квадрата.
Первый способ построения (Рис. 1). Проводим в окружности вертикальный и горизонтальный диаметры (Шаг 1).
Точки пересечения этих диаметров с окружностью являются вершинами квадрата (Шаг 2).

Второй способ построения (Рис. 2). Как и в первом способе проводим в окружности вертикальный и горизонтальный диаметры. Из точек пересечения диаметров с окружностью строим дуги с радиусом R, равным радиусу окружности (Шаг 1).
Точки пересечения дуг EG и FH соединяем соответственно линиями (Шаг 2). Точки пересечения этих линий с окружностью и являются вершинами квадрата.
Деление окружностей. Построение правильного шестиугольника.
В окружности радиуса R следует провести вертикальный диаметр (Шаг 1).
Из нижней точки пересечения диаметра с окружностью, как из центра следует провести дугу радиусом R (Шаг 2).

Аналогично, из верхней точки пересечения диаметра с окружностью следует провести дугу радиусом R (Шаг 3).
Соединяем все точки пересечения на окружности и в итоге получаем правильный шестиугольник (Шаг 4).

Деление окружностей. Построение равностороннего треугольника.
В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр.
Из нижней точки пересечения диаметра с окружностью, как из центра, тем же радиусом R следует провести дугу до пересечения с окружностью в точках C и B (Шаг 2).

Точки A,B и C на окружности являются вершинами равностороннего треугольника (Шаг 3).

Деление окружностей. Построение правильного пятиугольника.
Провести в окружности радиусом R два перпендикулярных диаметра (Шаг 1).
Из точек A и B , как из центра, следует провести две дуги радиусом R, до пересечения с окружностью (Шаг 2).

Длинна отрезков CE = CF = L является длинной стороны правильного пятиугольника. Четырьмя дугами радиусом L следует сделать засечки на окружности (Шаг 3).
Точка С и точки пересечения дуг с окружностью являются вершинами правильного пятиугольника (Шаг 4).

Деление окружностей. Построение правильного семиугольника.
Сторона правильного семиугольника приближенно равна 1/2 стороны правильного треугольника. Поэтому сначала следует построить основание правильного треугольника (Шаг 1).
Основание правильного треугольника AB делится пополам в точке С вертикальным диаметром окружности (Шаг 2). Длинна отрезка z = AC является длиной стороны правильного семиугольника.

Радиусом дуги равным z следует сделать на окружности засечки, как показано на рисунке (Шаг 3). Построения лучше начинать из верхней точки D.
Из точки D, последовательно следует соединить все точки пересечения дуг с окружностью. В итоге получаем правильный семиугольник (Шаг 4).

Сопряжения. Точка сопряжения.
Сопряжением называется такое соединение двух линий, при котором обеспечивается плавный переход одной линии в другую. Точка плавного перехода называется точкой сопряжения.

В точке сопряжения N прямой и окружности прямая является касательной к окружности. Две окружности в точке сопряжения имеют общую касательную. Точка сопряжения и центры касающихся окружностей лежат на одной прямой - точки O1, N1, O или точки O, O2, N2.

Сопряжение двух параллельных прямых дугой полуокружности.
Проведем прямую 3, перпендикулярную параллельным прямым 1 и 2 (Шаг 1).
Делим отрезок AB пополам (Шаг 2).

Проводим дугу полуокружности радиуса R = AO = OB, которая плавно соединяет данные параллельные прямые (Шаг 3).

Скругление прямого угла дугой радиуса R
Дан прямой угол и радиус дуги R (Шаг 1).
Из вершины угла, как из центра, проводим дугу данного радиуса R, которая пересекает стороны угла в точках B и C (Шаг 2).

Из точек В и С, как из центров, проводим дуги радиуса R до их пересечения в точке D (Шаг 3).
Дуга радиуса DB = R, проведенная между точками С и В, скругляет данный прямой угол (Шаг 4).

Скругление острого угла дугой радиуса R
Дан острый угол между прямыми 1 и 2 и радиус дуги R (Шаг 1).
Проведем прямые 3 и 4, соответственно параллельные сторонам 1 и 2 угла, на расстоянии R от них (Шаг 2).

Опустим перпендикуляры из точки О на стороны угла (Шаг 3).
Основания перпендикуляров В и С - это точки сопряжения. Проведем дугу ВС радиуса ОВ = R, которая скругляет данный угол (Шаг 4).

Сопряжение двух окружностей дугой данного радиуса R (1-й случай)
Проведем радиусами R1+R и R2+R две дуги 1 и 2, концентрические данным окружностям (Шаг 1).
Пересечение дуг 1 и 2 определяет центр сопряжения О. Проведем прямые ОО1 и ОО2, пересекающие данные окружности в точках сопряжения А1 и А2 (Шаг 2).

Из центра О радиусом ОА1 проведем дугу А1А2 (Шаг 3), которая плавно соединяет данные окружности.

Сопряжение двух окружностей дугой данного радиуса R (2-й случай)
Проведем радиусами R1-R и R2+R две дуги 1 и 2, концентрические данным окружностям. Пересечение дуг 1 и 2 определяет центр сопряжения О. Проведем прямые ОО1 и ОО2, пересекающие данные окружности в точках сопряжения А1 и А2 (Шаг 1).

Из центра О радиусом ОА1 проведем дугу А1А2, которая плавно соединяет данные окружности (Шаг 2).

Сопряжение прямой и окружности радиуса R дугой данного радиуса r (1-й случай)
Проведем прямую 3 параллельно прямой 1 на расстоянии r от нее и из центра О дугу 2 радиусом R+r (Шаг 1).


Проводим дугу АВ из центра О1 радиусом r, которая плавно соединяет прямую 1 и окружность радиуса R (Шаг 3).

Сопряжение прямой и окружности радиуса R дугой данного радиуса r (2-й случай r > R)
Проведем прямую 3 параллельно прямой 1 на расстоянии r от нее и из центра О дугу 2 радиусом r - R (Шаг 1).
Точка О1 пересечения дуги 2 и прямой 3 есть центр дуги радиуса r. Определим точки сопряжения А и В, опустив перпендикуляр из О1 на прямую 1 и соединив центры О и О1(Шаг 2).

Проводим дугу АВ из центра О1 радиусом r, которая плавно соединяет прямую 1 и окружность радиуса R (Шаг 3).