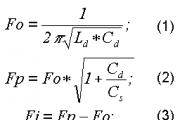Материальные уравнения электродинамики. Принцип действия

в произвольной среде. Максвелла уравнения сформулированы Дж. К. Максвеллом в 60-х годах 19 века на основе обобщения эмпирических законов электрических и магнитных явлений. Опираясь на эти законы и развивая плодотворную идею М. Фарадея о том, что взаимодействия между электрически заряженными телами осуществляются посредством электромагнитного поля , Максвелл создал теорию электромагнитных процессов, математически выражаемую Максвелла уравнения Современная форма Максвелла уравнения дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом .

Максвелла уравнения связывают величины, характеризующие электромагнитное поле, с его источниками, то есть с распределением в пространстве электрических зарядов и токов. В пустоте электромагнитное поле характеризуется двумя векторными величинами, зависящими от пространственных координат и времени: напряжённостью электрического поля Е и магнитной индукцией В . Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение которых в пространстве задаётся плотностью заряда r (зарядом в единице объёма) и плотностью тока j (зарядом, переносимым в единицу времени через единичную площадку, перпендикулярную направлению движения зарядов). Для описания электромагнитных процессов в материальной среде (в веществе), кроме векторов Е и В , вводятся вспомогательные векторные величины, зависящие от состояния и свойств среды: электрическая индукция D и напряжённость магнитного поля Н .

Максвелла уравнения позволяют определить основные характеристики поля (Е, В, D и Н ) в каждой точке пространства в любой момент времени, если известны источники поля j и r как функции координат и времени. Максвелла уравнения могут быть записаны в интегральной или в дифференциальной форме (ниже они даны в абсолютной системе единиц Гаусса; см. СГС система единиц ).

Максвелла уравнения в интегральной форме определяют по заданным зарядам и токам не сами векторы поля Е, В, D, Н в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик поля: циркуляцию векторов Е и Н вдоль произвольных замкнутых контуров и потоки векторов D и через произвольные замкнутые поверхности.

Первое Максвелла уравнения является обобщением на переменные поля эмпирического Ампера закона о возбуждении магнитного поля электрическими токами. Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения. Ток смещения возбуждает магнитное поле по тому же закону, что и ток проводимости (позднее это было подтверждено экспериментально). Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым.

Первое Максвелла уравнения имеет вид:

то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность j n - проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds , являющейся частью поверхности S, - проекция плотности тока смещения на ту же нормаль, а с = 3×10 10 см/сек - постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.

Второе Максвелла уравнения является математической формулировкой закона электромагнитной индукции Фарадея (см. Индукция электромагнитная ) записывается в виде:

, (1, б)

то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S , ограниченную данным контуром. Здесь n - проекция на нормаль к площадке ds вектора магнитной индукции В ; знак минус соответствует Ленца правилу для направления индукционного тока.

Третье Максвелла уравнения выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):

то есть поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.

Четвёртое Максвелла уравнения (обычно называемое Гаусса теоремой ) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов - Кулона закона :

, (1, г)

то есть поток вектора электрической индукции через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объёме , ограниченном данной поверхностью).

Если считать, что векторы электромагнитного поля (Е, В, D, Н ) являются непрерывными функциями координат, то, рассматривая циркуляцию векторов Н и Е по бесконечно малым контурам и потоки векторов и D через поверхности, ограничивающие бесконечно малые объёмы, можно от интегральных соотношений (1, а - г) перейти к системе дифференциальных уравнений, справедливых в каждой точке пространства, то есть получить дифференциальную форму Максвелла уравнения (обычно более удобную для решения различных задач):

rot,

Здесь rot и div - дифференциальные операторы ротор (см. Вихрь ) и дивергенция , действующие на векторы Н , Е , и D . Физический смысл уравнений (2) тот же, что и уравнений (1).

Максвелла уравнения в форме (1) или (2) не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Необходимо их дополнить соотношениями, связывающими векторы Е, Н, D, В и j , которые не являются независимыми. Связь между этими векторами определяется свойствами среды и её состоянием, причём D и j выражаются через Е , а - через Н :

D = D (E ), = (Н ), j = j (E ). (3)

Эти три уравнения называются уравнениями состояния, или материальными уравнениями; они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определённую форму. В вакууме D ºЕ и º Н . Совокупность уравнений поля (2) и уравнений состояния (3) образуют полную систему уравнений.

Макроскопические Максвелла уравнения описывают среду феноменологически, не рассматривая сложного механизма взаимодействия электромагнитного поля с заряженными частицами среды. Максвелла уравнения могут быть получены из Лоренца - Максвелла уравнений для микроскопических полей и определённых представлений о строении вещества путём усреднения микрополей по малым пространственно-временным интервалам. Таким способом получаются как основные уравнения поля (2), так и конкретная форма уравнений состояния (3), причём вид уравнений поля не зависит от свойств среды.

Уравнения состояния в общем случае очень сложны, так как векторы D , и j в данной точке пространства в данный момент времени могут зависеть от полей Е и Н во всех точках среды во все предшествующие моменты времени. В некоторых средах векторы D и могут быть отличными от нуля при Е и равных нулю (сегнетоэлектрики и ферромагнетики ). Однако для большинства изотропных сред, вплоть до весьма значительных полей, уравнения состояния имеют простую линейную форму:

D = eE , = mH , j = sE + j c тр. (4)

Здесь e (x, у, z ) - диэлектрическая проницаемость , а m (x, у, z ) - магнитная проницаемость среды, характеризующие соответственно её электрические и магнитные свойства (в выбранной системе единиц для вакуума e = m = 1); величина s(x, у, z ) называется удельной электропроводностью; j cтр - плотность так называемых сторонних токов, то есть токов, поддерживаемых любыми силами, кроме сил электрического поля (например, магнитным полем, диффузией и т. д.). В феноменологической теории Максвелла макроскопические характеристики электромагнитных свойств среды e, m и s должны быть найдены экспериментально. В микроскопической теории Лоренца - Максвелла они могут быть рассчитаны.

Проницаемости e и m фактически определяют тот вклад в электромагнитное поле, который вносят так называемые связанные заряды, входящие в состав электрически нейтральных атомов и молекул вещества. Экспериментальное определение e, m, s позволяет рассчитывать электромагнитное поле в среде, не решая трудную вспомогательную задачу о распределении связанных зарядов и соответствующих им токов в веществе. Плотность заряда r и плотность тока j в Максвелла уравнения - это плотности свободных зарядов и токов, причём вспомогательные векторы Н и D вводятся так, чтобы циркуляция вектора Н определялась только движением свободных зарядов, а поток вектора D - плотностью распределения этих зарядов в пространстве.

Если электромагнитное поле рассматривается в двух граничащих средах, то на поверхности их раздела векторы поля могут претерпевать разрывы (скачки); в этом случае уравнения (2) должны быть дополнены граничными условиями:

[nH ] 2 - [nH ] 1 = ,

[nE ] 2 - [nE ] 1 = 0, (5)

(nD ) 2 - (nD ) 1 = 4ps,

(nB ) 2 - (nB ) 1 = 0.

Здесь j пов и s - плотности поверхностных тока и заряда, квадратные и круглые скобки - соответственно векторное и скалярное произведения векторов, n - единичный вектор нормали к поверхности раздела в направлении от первой среды ко второй (1®2), а индексы относятся к разным сторонам границы раздела.

Основные уравнения для поля (2) линейны, уравнения же состояния (3) могут быть и нелинейными. Обычно нелинейные эффекты обнаруживаются в достаточно сильных полях. В линейных средах [удовлетворяющих соотношениям (4)] и, в частности, в вакууме Максвелла уравнения линейны и, таким образом, оказывается справедливым суперпозиции принцип : при наложении полей они не оказывают влияния друг на друга.

Из Максвелла уравнения вытекает ряд законов сохранения. В частности, из уравнений (1, а) и (1, г) можно получить соотношение (так называемое уравнение непрерывности):

, (6)

представляющее собой закон сохранения электрического заряда: полный ток, протекающий за единицу времени через любую замкнутую поверхность S , равен изменению заряда внутри объёма V , ограниченного этой поверхностью. Если ток через поверхность отсутствует, то заряд в объёме остаётся неизменным.

Из Максвелла уравнения следует, что электромагнитное поле обладает энергией и импульсом (количеством движения). Плотность энергии w (энергии единицы объёма поля) равна:

, (7)

Электромагнитная энергия может перемещаться в пространстве. Плотность потока энергии определяется так называемым вектором Пойнтинга

Направление вектора Пойнтинга перпендикулярно как Е , так и Н и совпадает с направлением распространения электромагнитной энергии, а его величина равна энергии, переносимой в единицу времени через единицу поверхности, перпендикулярной к вектору П . Если не происходит превращений электромагнитной энергии в другие формы, то, согласно Максвелла уравнения , изменение энергии в некотором объёме за единицу времени равно потоку электромагнитной энергии через поверхность, ограничивающую этот объём. Если внутри объёма за счёт электромагнитной энергии выделяется тепло, то закон сохранения энергии записывается в форме:

(9)

Где Q - количество теплоты, выделяемой в единицу времени.

Плотность импульса электромагнитного поля g (импульс единицы объёма поля) связана с плотностью потока энергии соотношением:

Существование импульса электромагнитного поля впервые было обнаружено экспериментально в опытах П. Н. Лебедева по измерению давления света (1899).

Как видно из (7), (8) и (10), электромагнитное поле всегда обладает энергией, а поток энергии и электромагнитный импульс отличны от нуля лишь в случае, когда одновременно существуют и электрическое и магнитное поля (причём эти поля не параллельны друг другу).

Максвелла уравнения приводят к фундаментальному выводу о конечности скорости распространения электромагнитных взаимодействий (равной с = 3×10 10 см/сек ). Это означает, что при изменении плотности заряда или тока в некоторой точке пространства порождаемое ими электромагнитное поле в точке наблюдения изменяется не в тот же момент времени, а спустя время t = R/c , где R - расстояние от элемента тока или заряда до точки наблюдения. Вследствие конечной скорости распространения электромагнитных взаимодействий возможно существование электромагнитных волн , частным случаем которых (как впервые показал Максвелл) являются световые волны.

Электромагнитные явления протекают одинаково во всех инерциальных системах отсчёта , то есть удовлетворяют принципу относительности. В соответствии с этим Максвелла уравнения не меняют своей формы при переходе от одной инерциальной системы отсчёта к другой (релятивистски инвариантны). Выполнение принципа относительности для электромагнитных процессов оказалось несовместимым с классическими представлениями о пространстве и времени, потребовало пересмотра этих представлений и привело к созданию специальной теории относительности (А. Эйнштейн , 1905; см. Относительности теория ). Форма Максвелла уравнения остаётся неизменной при переходе к новой инерциальной системе отсчёта, если пространств, координаты и время, векторы поля Е, Н, В, D , плотность тока j и плотность заряда r изменяются в соответствии с Лоренца преобразованиями (выражающими новые, релятивистские представления о пространстве и времени). Релятивистски-инвариантная форма Максвелла уравнения подчёркивает тот факт, что электрическое и магнитное поля образуют единое целое.

Максвелла уравнения описывают огромную область явлений. Они лежат в основе электротехники и радиотехники и играют важнейшую роль в развитии таких актуальных направлений современной физики, как физика плазмы и проблема управляемых термоядерных реакций , магнитная гидродинамика , нелинейная оптика , конструирование ускорителей заряженных частиц , астрофизика и т. д. Максвелла уравнения неприменимы лишь при больших частотах электромагнитных волн, когда становятся существенными квантовые эффекты, то есть когда энергия отдельных квантов электромагнитного поля - фотонов - велика и в процессах участвует сравнительно небольшое число фотонов.

Лит.: Максвелл Дж. К., Избранные сочинения по теории электромагнитного поля, перевод с английского, М., 1952; Тамм И. Е., Основы теории электричества, 7 изд., М., 1957; Калашников С. Г., Электричество, М., 1956 (Общий курс физики, т. 2); Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, (перевод с английского], в. 5, 6, 7, М., 1966; Ландау Л. Д., Лифшиц Е. М., Теория поля, 5 изд., М., 1967 (Теоретическая физика, т. 2); их же, Электродинамика сплошных сред, М., 1959.

Г. Я. Мякишев.

Статья про слово "Максвелла уравнения " в Большой Советской Энциклопедии была прочитана 34382 раз

Введение Максвеллом понятия тока смещения, привело к завершению созданной им макроскопической теории электромагнитного поля, которая позволяет с единой точки зрения объяснить не только электрические и магнитные явления, но и предсказать новые, существования которых было впоследствии подтверждено.

В основе теории Максвелла лежат 4 уравнения:

1. Электрическое поле может быть как потенциальным, так и вихревым, поэтому напряженность результирующего поля равна:

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля :

Получаем

Итак, полная система уравнений Максвелла в интегральной форме:

	1),
	2),

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует связь.

Для изотропных, несегнетоэлектрических и неферромагнитных сред запишем формулы связи:

	б) ,
	в) ,

где - электрическая постоянная, - магнитная постоянная,

Диэлектрическая проницаемость среды, m - магнитная проницаемость среды,

r - удельное электрическое сопротивление, - удельная электрическая проводимость.

Из уравнений Максвелла вытекает, что:

источником электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, которые могут возбуждаться либо движущимися электрическими зарядами (токами), либо переменными электрическими полями.

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе не существует магнитных зарядов.

Если и (стационарные поля), то уравнения Максвелла принимают следующий вид:

Источниками электрического стационарного поля являются только электрические заряды, источниками стационарного магнитного поля - только токи проводимости.

Электрическое и магнитное поле в данном случае независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Дифференциальная форма записи уравнений Максвелла:

	3) ,

Интегральная форма записи уравнений Максвелла является более общей, если имеются поверхности разрыва. Дифференциальная форма записи уравнения Максвелла предполагает, что все величины в пространстве и времени изменяются непрерывно.

Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же важную роль, как и законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с переменным электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным полем, т.е. электрическое и магнитное поле неразрывно связаны друг с другом – они образуют единое электромагнитное поле.

Свойства уравнений Максвелла

Уравнения Максвелла линейны. Они содержат только первые производные полей Е и В по времени и пространственным координатам и первые степени плотности электрических зарядов и токов j . Свойство линейности уравнений Максвелла связано с принципом суперпозиции, если два каких-нибудь поля удовлетворяют уравнениям Максвелла, то это относится и к сумме этих полей.

Уравнения Максвелла содержат уравнения непрерывности, выражающие закон сохранения электрического заряда. Чтобы получить уравнение непрерывности необходимо взять дивергенцию от обеих частей первого из уравнений Максвелла в дифференциальной форме записи:

Уравнения Максвелла выполняются во всех инерциальных системах отсчета. Они являются релятивистки инвариантными. Это есть следствие принципа относительности, согласно которому все инерциальные системы отсчета физически эквивалентны друг другу. Вид уравнений Максвелла при переходе от одной инерциальной системы отсчета к другой не меняется, однако входящие в них величины преобразуются по определенным правилам. Т.е. уравнения Максвелла являются правильными релятивистскими уравнениями в отличие, например, от уравнений механики Ньютона.

Уравнения Максвелла несимметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе электрические заряды существуют, а магнитные заряды нет.

Из уравнений Максвелла следует важный вывод о существовании принципиально нового явления: электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов. При этом изменение его имеет обязательно волновой характер. Поля такого рода называют электромагнитными волнами. В вакууме они всегда распространяются со скоростью равной скорости света. Теория Максвелла предсказала существование электромагнитных волн и позволила установить все их основные свойства.

Ток смещения. Для обобщения уравнений электромагнитного поля в вакууме на переменные поля необходимо изменить только одно из написанных ранее уравнений (см. разд. 3.4, 3.12); три уравнения оказываются верными в общем случае. Однако закон полного тока для магнитного поля в случае переменных полей и токов оказывается неверным. В соответствии с этим законом ток должен быть одинаковым для любых двух натянутых на контур поверхностей; если заряд в объеме между выбранными поверхностями меняется, то это утверждение вступает в противоречие с законом сохранения заряда. Например, при зарядке конденсатора (рис. 45) ток через одну из указанных поверхностей равен а через другую (проходящую между пластинами) - нулю. Чтобы снять указанное противоречие, Максвелл ввел в это уравнение ток смещения, пропорциональный скорости изменения электрического поля:

В диэлектрической среде выражение для тока смещения принимает вид:

Первый член представляет собой плотность тока смещения в вакууме, второй - реальный ток, обусловленный движением связанных зарядов при изменении поляризованности. Ток смещения через поверхность равен где Ф - поток вектора через поверхность. Введение тока смещения снимает противоречие с законом сохранения заряда. Например, при зарядке плоского конденсатора ток смещения через поверхность, проходящую между пластинами, равен току по подводящим проводам.

Система уравнений Максвелла в вакууме. После введения тока смещения система уравнений Максвелла в дифференциальной форме принимает вид:

Система уравнений Максвелла в интегральной форме:

Приведем также запись уравнений Максвелла в дифференциальной форме в системе СГС:

Плотности заряда и тока связаны соотношением

выражающим закон сохранения заряда (это уравнение является следствием уравнений Максвелла).

Уравнения Максвелла в среде имеют вид: дифференциальная форма интегральная форма

и служат для определения четырех величин . К уравнениям Максвелла, в среде надо добавить материальные уравнения связи между , характеризующие электрические и магнитные свойства среды. Для изотропных линейных сред эти уравнения имеют вид:

Из уравнений Максвелла можно получить граничные условия для (см. разд. 3.6, 3.13).

Закон сохранения энергии для электромагнитного поля.

Из уравнений Максвелла можно вывести следующее уравнение для любого объема V, ограниченного поверхностью

Первый член описывает изменение энергии электромагнитного поля в рассматриваемом объеме. Видно, что в общем случае для плотности энергии электромагнитного поля оказываются верными формулы, полученные ранее для постоянного электрического и магнитного полей. Второй член представляет собой работу поля над частицами в рассматриваемом объеме. Наконец, третий член описывает поток электромагнитной энергии через ограничивающую объем замкнутую поверхность. Плотность потока энергии в данной точке пространства (вектор Пойнтинга) определяется векторами Е и В в этой же точке:

Последнее выражение справедливо и для плотности потока электромагнитной энергии в веществе. Плотность энергии в среде имеет вид:

Пример 1. Рассмотрим зарядку плоского конденсатора с круглыми пластинами, расположенными на расстоянии . Скорость изменения энергии в цилиндре радиусом (меньше размеров пластин) равна

Напряженность магнитного поля найдем из второго уравнения Максвелла: (справа стоит ток смещения). Получаем, что скорость притока энергии через боковую поверхность цилиндра: равна скорости изменения энергии в объеме.

Релятивистские свойства полей. При переходе из одной инерциальной системы отсчета в другую изменяются как источники электромагнитного поля (плотности заряда и тока), так и сами поля, но уравнения Максвелла сохраняют свой вид. Проще всего выглядят формулы преобразования для источников - плотность движущегося заряда). Если обозначить за плотность заряда в ИСО, в которой то с учетом сокращения продольных размеров (см. разд. 1.11) получим

Сравнивая с -вектором энергии-импульса, видим, что образуют -вектор, т.е. преобразуются друг через друга так же, как по формулам преобразования Лоренца. Зная, как преобразуются источники поля, можно найти формулы для преобразования Е, В. Они выглядят так:

Здесь - скорость системы отсчета К относительно системы К, преобразования записаны для компонент полей, параллельных и перпендикулярных Инвариантами этих преобразований являются скалярные величины

При с формулы преобразования полей принимают следующий упрощенный вид:

Пример 2. Магнитное поле нерелятивистской частицы. Рассмотрим частицу, которая движется относительно ИСО К с постоянной нерелятивистской скоростью V. В ИСО связанной с движущейся частицей, имеется только электрическое поле Для перехода в ИСО К надо записать формулы

преобразования Учитывая, что в нерелятивистском пределе длины отрезков не меняются, получим (для момента, когда частица проходи в К через начало координат):

При выводе этих формул было использовано равенство

Пример 3. Поляризация диэлектрика при движении в магнитном поле. При движении диэлектрика с нерелятивистской скоростью перпендикулярно линиям индукции магнитного поля происходит его поляризация. В ИСО, связанной с диэлектриком, существует поперечное электрическое поле . Характер поляризации диэлектрика зависит от его формы.

Пример 4. Электрическое поле релятивистской частицы. Рассмотрим частицу, которая движется относительно ИСО К с постоянной релятивистской скоростью V. В ИСО К связанной с движущейся частицей, имеется только электрическое поле Для перехода в ИСО К следует использовать формулы преобразования (92) с Запишем ответ для момента времени, когда частица в ИСО К проходит через начало координат, для точки, лежащей в плоскости При переходе от координат к координатам надо учесть, что (координаты точки измеряются в К одновременно с прохождением частицы через начало координат). В результате получим

Видно, что вектор Е коллинеарен вектору Однако на одном и том же расстоянии от заряда поле в точке, расположенной На линии его движения, меньше, чем в точке, расположенной на перпендикуляре к скорости. Магнитное поле в той же точке определяется выражением:

Отметим, что рассмотренное электрическое поле не является потенциальным.

Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь сэлектрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики . Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом , но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).

Содержание [убрать] 1. История 2. Запись уравнений Максвелла и системы единиц 3. Дифференциальная форма 4. Интегральная форма 5. Сила Лоренца 6. Размерные константы в уравнениях Максвелла 7. Уравнения Максвелла в среде 7.1 Связанные заряды и токи 7.2 Материальные уравнения 7.3 Уравнения в изотропных и однородных средах без дисперсии o 7.4 Граничные условия 8. Законы сохранения 8.1 Уравнение непрерывности o 8.2 Закон сохранения энергии 9. Потенциалы 9.1 Скалярный и векторный потенциалы 9.2 Векторы Герца 9.3 Потенциалы Дебая 9.4 Векторы Римана — Зильберштейна 10. Ковариантная формулировка o 10.1 Четырёхмерные векторы 10.2 Тензор электромагнитного поля o 10.3 Лагранжиан 10.4 Запись при помощи дифференциальных форм 10.5 Общековариантная запись в компонентах 11. Спектральное представление 12. Уравнения без свободных зарядов и токов 12.1 Волновое уравнение 12.2 Уравнение Гельмгольца 13. Некоторые точные решения 13.1 Поле движущегося точечного заряда 13.2 Плоские электромагнитные волны 14. Связь с другими теориями 15. Аксиоматический подход 16. Единственность решений уравнений Максвелла 17. Численное решение уравнений Максвелла 18. Источники 19. Примечания 20. См. также 21. Литература 21.1 Исторические публикации 21.2 История развития 21.3 Общие курсы физики 21.4 Курсы теоретической физики 21.5 Решения уравнений Максвелла 22. Ссылки

История

Уравнения, сформулированные Джеймсом Клерком Максвеллом, возникли на основе ряда важных экспериментальных открытий, которые были сделаны в начале XIX века. В 1820 году Ганс Христиан Эрстед обнаружил, что пропускаемый через проводгальванический ток заставляет отклоняться магнитную стрелку компаса. Это открытие привлекло широкое внимание учёных того времени. В том же 1820 году Био и Савар экспериментально нашли выражение для порождаемой током магнитной индукции (закон Био-Савара ), и Андре Мари Ампер обнаружил, чтовзаимодействие на расстоянии возникает также между двумя проводниками, по которым пропускается ток. Ампер ввёл термин «электродинамический» и выдвинул гипотезу, что природный магнетизм связан с существованием в магните круговых токов.

Влияние тока на магнит, обнаруженное Эрстедом, привело Майкла Фарадея к идее о том, что должно существовать обратное влияние магнита на токи. После длительных экспериментов, в 1831 году, Фарадей открыл, что перемещающийся возле проводника магнит порождает в проводнике электрический ток. Это явление было названо электромагнитной индукцией. Фарадей ввёл понятие «поля сил» — некоторой среды, находящейся между зарядамии токами. Его рассуждения носили качественный характер, однако они оказали огромное влияние на исследования Максвелла.

После открытий Фарадея стало ясно, что старые модели электромагнетизма (Ампер, Пуассон и др.) неполны. Вскоре появилась теория Вебера, основанная на дальнодействии. Однако к этому моменту вся физика, кроме теории тяготения, имела дело только с близкодейственными силами (оптика, термодинамика, механика сплошных сред и др.). Гаусс, Риман и ряд других учёных высказывали догадки, что свет имеет электромагнитную природу, так что теория электромагнитных явлений тоже должна быть близкодейственной. Этот принцип стал существенной особенностью теории Максвелла.

В своём знаменитом «Трактате об электричестве и магнетизме» (1873) Максвелл писал:

"Приступая к изучению труда Фарадея, я установил, что его метод понимания явлений был так же математическим, хотя и не представленным в форме обычных математических символов. Я также нашёл, что этот метод можно выразить в обычной математической форме и таким образом сравнить с методами профессиональных математиков".

Заменяя фарадеевский термин «поле сил» на понятие «напряжённость поля», Максвелл сделал его ключевым объектом своей теории:

Если мы примем эту среду в качестве гипотезы, я считаю, что она должна занимать выдающееся место в наших исследованиях, и что нам следовало бы попытаться сконструировать рациональное представление о всех деталях её действия, что и было моей постоянной целью в этом трактате.

Подобная электродинамическая среда явилась абсолютно новым понятием для ньютоновской физики. Последняя изучала взаимодействие между собой материальных тел. Максвелл же записал уравнения, которым должна подчиняться среда, определяющая взаимодействие зарядов и токов и существующая даже в их отсутствие.

Электрический ток создаёт магнитную индукцию (закон Ампера )

Анализируя известные эксперименты, Максвелл получил систему уравнений для электрического и магнитного полей. В 1855 году в своей самой первой статье «О фарадеевых силовых линиях» («On Faraday’s Lines of Force») он впервые записал в дифференциальной форме систему уравнений электродинамики, но не вводя ещё ток смещения. Такая система уравнений описывала все известные к тому времени экспериментальные данные, но не позволяла связать между собой заряды и токи и предсказатьэлектромагнитные волны. Впервые ток смещения был введён Максвеллом в работе «О физических силовых линиях» («On Physical Lines of Force»), состоящей из четырёх частей и опубликованной в 1861-1862 годах.

Обобщая закон Ампера, Максвелл вводит ток смещения, вероятно, чтобы связать токи и заряды уравнением непрерывности, которое уже было известно для других физических величин. Следовательно, в этой статье фактически была завершена формулировка полной системы уравнений электродинамики. В статье 1864 года «Динамическая теория электромагнитного поля» («A dynamical theory of the electromagnetic field») рассмотрена сформулированная ранее система уравнений из 20 скалярных уравнений для 20 скалярных неизвестных. В этой статье Максвелл впервые сформулировал понятие электромагнитного поля как физической реальности, имеющей собственную энергию и конечное время распространения, определяющее запаздывающий характер электромагнитного взаимодействия.

Переменный поток магнитного поля создаёт электрическое поле (закон Фарадея )

Оказалось, что не только ток, но и изменяющееся со временем электрическое поле (ток смещения) порождаетмагнитное поле. В свою очередь, в силу закона Фарадея, изменяющееся магнитное поле снова порождает электрическое. В результате, в пустом пространстве может распространяться электромагнитная волна. Из уравнений Максвелла следовало, что её скорость равна скорости света, поэтому Максвелл сделал вывод об электромагнитной природе света.

Часть физиков выступила против теории Максвелла (особенно много возражений вызвала концепция тока смещения). Гельмгольц предложил свою теорию, компромиссную по отношению к моделям Вебера и Максвелла, и поручил своему ученику Генриху Герцу провести её экспериментальную проверку. Однако опыты Герца однозначно подтвердили правоту Максвелла.

Максвелл не использовал векторных обозначений и записывал свои уравнения в достаточно громоздком компонентном виде. В своём трактате он, кроме того, частично использовалкватернионную формулировку. Современная форма уравнений Максвелла появилась около 1884 года после работ Хевисайда, Герца и Гиббса. Они не только переписали систему Максвелла в векторном виде, но и симметризовали её, переформулировав в терминах поля, избавившись отэлектрического и магнитного потенциалов, игравших в теории Максвелла существенную роль, поскольку полагали, что эти функции являются лишь ненужными вспомогательными математическими абстракциями. Интересно, что современная физика поддерживает Максвелла, но не разделяет негативное отношение его ранних последователей к потенциалам.Электромагнитный потенциал играет важную роль в квантовой физике и проявляется как физически измеряемая величина в некоторых экспериментах, например, в эффекте Ааронова-Бома.

Система уравнений в формулировке Герца и Хевисайда некоторое время называлась уравнениями Герца-Хевисайда. Эйнштейн в классической статье «К электродинамике движущихся тел» назвал их уравнениями Максвелла-Герца. Иногда в литературе встречается также название уравнения Максвелла-Хевисайда.

Уравнения Максвелла сыграли важную роль при возникновении специальной теории относительности (СТО). Джозеф Лармор (1900 год) и независимо от него Хенрик Лоренц (1904 год) нашли преобразования координат, времени и электромагнитных полей, которые оставляют уравнения Максвелла инвариантными при переходе от одной инерциальной системы отсчёта к другой. Эти преобразования отличались от преобразований Галилея классической механики и, следуя Анри Пуанкаре, стали называться преобразованиями Лоренца. Они стали математическим фундаментом специальной теории относительности.

Распространение электромагнитных волн со скоростью света первоначально интерпретировалось как возмущения некоторой среды, так называемого эфира. Были предприняты многочисленные попытки (см. исторический обзор) обнаружить движение Земли относительно эфира, однако они неизменно давали отрицательный результат. Поэтому Анри Пуанкаре высказал гипотезу о принципиальной невозможности обнаружить подобное движение (принцип относительности). Ему же принадлежит постулат о независимости скорости света от скорости его источника и вывод (вместе с Лоренцем), исходя из сформулированного так принципа относительности, точного видапреобразований Лоренца (при этом были показаны и групповые свойства этих преобразований).

Эти две гипотезы (постулата) легли и в основу статьи Альберта Эйнштейна (1905 год). С их помощью он также вывел преобразования Лоренца и утвердил их общефизический смысл, особо подчеркнув возможность их применения для перехода из любой инерциальной системы отсчета в любую другую инерциальную. Эта работа фактически ознаменовала собой построение специальной теории относительности. В СТО преобразования Лоренца отражают общие свойства пространства и времени, а модель эфира оказывается ненужной. Электромагнитные поля являются самостоятельными объектами, существующими наравне с материальными частицами.

Классическая электродинамика, основанная на уравнениях Максвелла, лежит в основе многочисленных приложений электро- и радиотехники, СВЧ и оптики. До настоящего времени не было обнаружено ни одного эффекта, который потребовал бы видоизменения уравнений. Они оказываются применимы и в квантовой механике, когда рассматривается движение, например, заряженных частиц во внешних электромагнитных полях. Поэтому уравнения Максвелла являются основой микроскопического описания электромагнитных свойств вещества.

Уравнения Максвелла востребованы также в астрофизике и космологии, поскольку многие планетыи звезды обладают магнитным полем. Магнитное поле определяет, в частности, свойства таких объектов, как пульсары и квазары.

На современном уровне понимания все фундаментальные частицы являются квантовыми возбуждениями («квантами») различных полей. Например, фотон — это квант электромагнитного поля, а электрон — квант спинорного поля. Поэтому полевой подход, предложенный Фарадеем и существенно развитый Максвеллом, является основой современной физики фундаментальных частиц, в том числе ее стандартной модели.

Исторически несколько раньше он сыграл важную роль в появлении квантовой механики в формулировке Шрёдингера и вообще открытии квантовых уравнений, описывающих движение частиц, в том числе и релятивистских (уравнение Клейна-Гордона, уравнение Дирака), хотя первоначально аналогия с уравнениями Максвелла здесь виделась скорее лишь в общей идее, тогда как впоследствии оказалось, что она может быть понята как более конкретная и детальная (как это описано выше).

Также полевой подход, в целом восходящий к Фарадею и Максвеллу, стал центральным в теории гравитации (включая ОТО).

Запись уравнений Максвелла и системы единиц

Запись большинства уравнений в физике не зависит от выбора системы единиц. Однако в электродинамике это не так. В зависимости от выбора системы единиц в уравнениях Максвелла возникают различные коэффициенты (константы). Международная система единиц СИ является стандартом в технике и преподавании, однако споры среди физиков о её достоинствах и недостатках по сравнению с конкурирующей симметричной гауссовой системой единиц (СГС) не утихают. Преимущество системы СГС в электродинамике состоит в том, что все поля в ней имеют одну размерность, а уравнения, по мнению многих учёных, записываются проще и естественней.

Поэтому СГС продолжает применяться в научных публикациях по электродинамике и в преподавании теоретической физики, например, в курсе теоретической физики Ландау и Лифшица . Однако для практических применений вводимые в СГС единицы измерений, многие из которых неименованы и неоднозначны, часто неудобны. Система СИ стандартизована и лучше самосогласованна, на этой системе построена вся современная метрология. Кроме того, система СИ обычно используется в курсах общей физики. В связи с этим все соотношения, если они по-разному записываются в системах СИ и СГС, далее приводятся в двух вариантах.

Дифференциальная форма

Уравнения Максвелла представляют собой в векторной записи систему из четырех уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных) линейных дифференциальных уравнений в частных производных 1-го порядка для 12 компонент четырёх векторных функций ():

Название	СГС	СИ	Примерное словесное выражение
Закон Гаусса			Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля			Не существуетмагнитных зарядов. [~ 1]
Закон индукции Фарадея			Изменение магнитной индукции порождает вихревое электрическое поле. [~ 1]
Теорема о циркуляции магнитного поля			Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

— плотность стороннего электрического заряда (в единицах СИ — Кл/м³);

— плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае - случае тока, порождаемого одним типом носителей заряда, она выражается просто как , где — (средняя) скорость движения этих носителей в окрестности данной точки, ρ 1 - плотность заряда этого типа носителей (она в общем случае не совпадает с ρ); в общем случае это выражение надо усреднить по разным типам носителей;

— скорость света в вакууме (299 792 458 м/с);

— напряжённость электрического поля (в единицах СИ — В/м);

— напряжённость магнитного поля (в единицах СИ — А/м);

— электрическая индукция (в единицах СИ — Кл/м²);

— магнитная индукция (в единицах СИ — Тл = Вб/м² = кг.с −2 .А −1);

— дифференциальный оператор набла, при этом:

Означает ротор вектора,

Означает дивергенцию вектора.

Приведённые выше уравнения Максвелла не составляют ещё полной системы уравненийэлектромагнитного поля, поскольку они не содержат свойств среды, в которой возбужденоэлектромагнитное поле. Соотношения, связывающие величины , , , и и учитывающие индивидуальные свойства среды, называются материальными уравнениями.

Интегральная форма

При решении уравнений Максвелла распределения зарядов и токов часто считаются заданными. С учётом граничных условий и материальных уравнений это позволяет определить напряжённость электрического поля и магнитную индукцию , которые, в свою очередь, определяют силу, действующую на пробный заряд , двигающийся со скоростью .

Эта сила называется силой Лоренца :

СГС	СИ

Электрическая составляющая силы направлена по электрическому полю (если ), а магнитная — перпендикулярна скорости заряда и магнитной индукции. Впервые выражение для силы, действующей на заряд в магнитном поле (электрическая компонента была известна), получил в 1889 году Хевисайд за три года до Хендрика Лоренца, который вывел выражение для этой силы в 1892 году.

В более сложных ситуациях в классической и квантовой физике в случае, когда под действием электромагнитных полей свободные заряды перемещаются и изменяют значения полей, необходимо решение самосогласованной системы из уравнений Максвелла и уравнений движения, включающих силы Лоренца. Получение точного аналитического решения такой полной системы сопряжено обычно с большими сложностями.

Размерные константы в уравнениях Максвелла

В гауссовой системе единиц СГС все поля имеют одинаковую размерность, и в уравнениях Максвелла фигурирует единственная фундаментальная константа , имеющая размерностьскорости, которая сейчас называется скоростью света (именно равенство этой константы скорости распространения света дало Максвеллу основания для гипотезы об электромагнитной природе света).

В системе единиц СИ, чтобы связать электрическую индукцию и напряжённость электрического поля в вакууме , вводится электрическая постоянная ε 0 (). Магнитная постоянная является таким же коэффициентом пропорциональности для магнитного поля в вакууме (). Названия электрическая постоянная и магнитная постоянная сейчас стандартизованы. Ранее для этих величин также использовались, соответственно, названия диэлектрическая и магнитная проницаемости вакуума.

Скорость электромагнитного излучения в вакууме (скорость света) в СИ появляется при выводеволнового уравнения:

В системе единиц СИ, в качестве точных размерных констант определены скорость света в вакууме и магнитная постоянная . Через них выражается электрическая постоянная ε 0 .

Принятые значения скорости света, электрической и магнитной постоянных приведены в таблице:

Иногда вводится величина, называемая «волновым сопротивлением», или «импедансом» вакуума:

Ом.

Приближённое значение для получается, если для скорости света принять значение м/c. В системе СГС . Эта величина имеет смысл отношения амплитуд напряжённостей электрического и магнитного полей плоской электромагнитной волны в вакууме.

Уравнения Максвелла в среде

Чтобы получить полную систему уравнений электродинамики, к системе уравнений Максвелла необходимо добавить материальные уравнения, связывающие величины , , , , , в которых учтены индивидуальные свойства среды. Способ получения материальных уравнений дают молекулярные теории поляризации, намагниченности и электропроводности среды, использующие идеализированные модели среды. Применяя к ним уравнения классической иликвантовой механики, а также методы статистической физики, можно установить связь между векторами , , с одной стороны и , с другой стороны.

Связанные заряды и токи

Слева : Совокупность микроскопических диполей в среде образуют один макроскопический дипольный момент и эквивалентны двум заряженным с противоположным знаком пластинам на границе. При этом внутри среды все заряды скомпенсированы;

Справа : Совокупность микроскопических циркулярных токов в среде эквивалентна макроскопическому току, циркулирующему вдоль границы. При этом внутри среды все токи скомпенсированы.

При приложении электрического поля кдиэлектрическому материалу каждая из его молекул превращается в микроскопическийдиполь. При этом положительные ядра атомов немного смещаются в направлении поля, а электронные оболочки в противоположном направлении. Кроме этого, молекулы некоторых веществ изначально имеют дипольный момент. Дипольные молекулы стремятся ориентироваться в направлении поля. Этот эффект называетсяполяризацией диэлектриков. Такое смещение связанных зарядов молекул в объёме эквивалентно появлению некоторого распределения зарядов на поверхности, хотя все молекулы, вовлечённые в процесс поляризации остаются нейтральными (см. рисунок).

Аналогичным образом происходит магнитная поляризация (намагнивание) в материалах, в которых составляющие их атомы и молекулы имеютмагнитные моменты, связанные со спином и орбитальным моментом ядер и электронов. Угловые моменты атомов можно представить в виде циркулярных токов. На границе материала совокупность таких микроскопических токов эквивалентна макроскопическим токам, циркулирующим вдоль поверхности, несмотря на то, что движение зарядов в отдельных магнитных диполях происходит лишь в микромасштабе (связанные токи).

Рассмотренные модели показывают, что хотя внешнее электромагнитное поле действует на отдельные атомы и молекулы, его поведение во многих случаях можно рассматривать упрощённым образом в макроскопическом масштабе, игнорируя детали микроскопической картины.

В среде сторонние электрические и магнитные поля вызывают поляризацию и намагничивание вещества, которые макроскопически описываются соответственно вектором поляризации ивектором намагниченности вещества, а вызваны появлением связанных зарядов и токов . В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.

Поэтому, выражая векторы и через , , и , можно получить математически эквивалентную систему уравнений Максвелла:

СГС	СИ

Индексом здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в , , а затем в и, следовательно, в сложный микроскопический характер электромагнитного поля в среде.

Материальные уравнения

Материальные уравнения устанавливают связь между и . При этом учитываются индивидуальные свойства среды. На практике в материальных уравнениях обычно используются экспериментально определяемые коэффициенты (зависящие в общем случае от частоты электромагнитного поля), которые собраны в различных справочниках физических величин.

В слабых электромагнитных полях, сравнительно медленно меняющихся в пространстве и вовремени, в случае изотропных, неферромагнитных и несегнетоэлектрических сред справедливо приближение, в котором поляризуемость и намагниченность линейно зависят от приложенных полей:

СГС	СИ

где введены безразмерные константы: — диэлектрическая восприимчивость и —магнитная восприимчивость вещества (в системе единиц СИ эти константы в раз больше, чем в гауссовой системе СГС). Соответственно, материальные уравнения для электрической и магнитной индукций записываются в следующем виде:

СГС	СИ

где — относительная диэлектрическая проницаемость, — относительная магнитная проницаемость. Размерные величины ε 0 ε (в единицах СИ — Ф/м) и μ 0 μ (в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость иабсолютная магнитная проницаемость соответственно.

В проводниках существует связь между плотностью тока и напряжённостью электрического поля, выражаемая законом Ома :

где — удельная проводимость среды (в единицах СИ — Ом −1 .м −1).

В анизотропной среде ε, и являются тензорами , и . В системе координат главных осей они могут быть описаны диагональными матрицами. В этом случае, связь между напряжённостями полей и индукциями имеют различные коэффициенты по каждой координате.

Например, в системе СИ:

Хотя для широкого класса веществ линейное приближение для слабых полей выполняется с хорошей точностью, в общем случае зависимость между и может быть нелинейной. В этом случае проницаемости среды не являются константами, а зависят от величины поля в данной точке. Кроме того, более сложная связь между и наблюдается в средах с пространственной или временной дисперсиями. В случае пространственной дисперсии токи и заряды в данной точке пространства зависят от величины поля не только в той же точке, но и в соседних точках. В случае временной дисперсии поляризация и намагниченность среды не определяются только величиной поля в данный момент времени, а зависят также от величины полей в предшествующие моменты времени. В самом общем случае нелинейных и неоднородных сред с дисперсией, материальные уравнения в системе СИ принимают интегральный вид:

Аналогичные уравнения получаются в гауссовой системе СГС (если формально положить ε 0 = 1).

Уравнения в изотропных и однородных средах без дисперсии

В изотропных и однородных средах без дисперсии уравнения Максвелла принимают следующий вид :

СГС	СИ

В оптическом диапазоне частот вместо диэлектрической проницаемости ε используется показатель преломления (зависящий от длины волны), показывающий отличие скорости распространения монохроматической световой волны в среде от скорости света в вакууме. При этом в оптическом диапазоне диэлектрическая проницаемость обычно заметно меньше чем на низких частотах, а магнитная проницаемость большинства оптических сред практически равна единице. Показатель преломления большинства прозрачных материалов составляет от 1 до 2, достигая 5 у некоторых полупроводников. В вакууме и диэлектрическая, и магнитная проницаемости равны единице: ε = μ = 1.

Поскольку уравнения Максвелла в линейной среде являются линейными относительно полей и свободных зарядов и токов , справедлив принцип суперпозиции:

Если распределения зарядов и токов создают электромагнитное поле с компонентами , а другие распределения создают, соответственно, поле , то суммарное поле, создаваемое источниками , будет равно .

При распространении электромагнитных полей в линейной среде в отсутствие зарядов и токовсумма любых частных решений уравнений будет также удовлетворять уравнениям Максвелла.

Граничные условия

Во многих случаях неоднородную среду можно представить в виде совокупности кусочно-непрерывных однородных областей, разделённых бесконечно тонкими границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая» на границах получающиеся решения. В частности, при рассмотрении решения в конечном объёме необходимо учитывать условия на границах объёма с окружающим бесконечным пространством. Граничные условия получаются из уравнений Максвелла предельным переходом. Для этого проще всего воспользоваться уравнениями Максвелла в интегральной форме.

Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно получить следующую связь между компонентами поля в двух областях, примыкающих к границе:

СГС	СИ
, ,	, ,

где — единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине, — плотность поверхностных свободных токов вдоль границы (то есть не включая связанных токов намагничивания, складывающихся на границе среды из микроскопических молекулярных итп токов). Первое граничное условие можно интерпретировать как непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля (из второго следует, что тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе).

Введение Максвеллом понятия тока сме­щения привело его к завершению создан­ной им единой макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование кото­рых было впоследствии подтверждено.

В основе теории Максвелла лежат рас­смотренные выше четыре уравнения:

1. Электрическое поле (см. § 137) мо­жет быть как потенциальным (e q), так и вихревым (Е B), поэтому напряженность суммарного поля Е =Е Q +Е B . Так как циркуляция вектора e q равна нулю (см. (137.3)), а циркуляция вектора Е B оп­ределяется выражением (137.2), то цир­куляция вектора напряженности суммар­ного поля

Это уравнение показывает, что источни­ками электрического поля могут быть не только электрические заряды, но и меняю­щиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

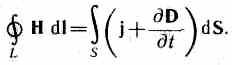
Это уравнение показывает, что магнит­ные поля могут возбуждаться либо дви­жущимися зарядами (электрическими то­ками), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

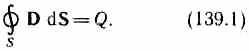
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью , то формула (139.1) запишется в виде

4. Теорема Гаусса для поля В (см. (120.3)):

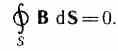
И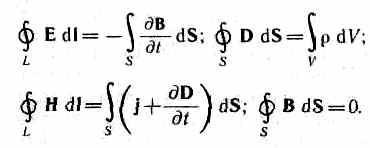так,полная система уравнений Максвел­ла в интегральной форме:

Величины, входящие в уравнения Мак­свелла, не являются независимыми и меж­ду ними существует следующая связь (изотропные не сегнетоэлектрические и не ферромагнитные среды):

D = 0 E ,

В=  0 Н,

j =E ,

где  0 и  0 - соответственно электриче­ская и магнитная постоянные,  и  - соответственно диэлектрическая и магнит­ная проницаемости,  - удельная прово­димость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля мо­гут быть либо электрические заряды, либо изменяющиеся во времени магнитные по­ля, а магнитные поля могут возбуждаться либо движущимися электрическими заря­дами (электрическими токами), либо пере­менными электрическими полями. Уравне­ния Максвелла не симметричны относи­тельно электрического и магнитного полей. Это связано с тем, что в природе су­ществуют электрические заряды, но нет зарядов магнитных.

Д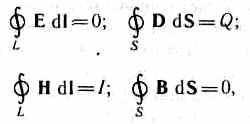ля стационарных полей (Е= const и В =const) уравнения Максвелла при­мут вид

т. е. источниками электрического поля в данном случае являются только электри­ческие заряды, источниками магнитно­го - только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электриче­ское и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса м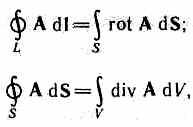ожно представитьполную систему урав­нений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла - интегральная

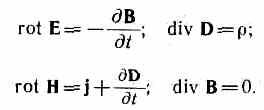идифференциальная - эквивалентны. Однако когда имеютсяповерхности разры­ва - поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений являет­ся более общей.

Уравнения Максвелла в дифференци­альной форме предполагают, что все вели­чины в пространстве и времени изменяют­ся непрерывно. Чтобы достичь математи­ческой эквивалентности обеих форм урав­нений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электро­магнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):

D 1 n = D 2 n , E 1  = E 2  , B 1 n = B 2 n , H 1  = H 2 

(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов прово­димости).

Уравнения Максвелла - наиболее об­щие уравнения для электрических и маг­нитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в ме­ханике. Из уравнений Максвелла следует, что переменное магнитное поле всегда свя­зано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнит­ным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом - они образуют единое электромагнитное поле.

Теория Максвелла, являясь обобщени­ем основных законов электрических и маг­нитных явлений, смогла объяснить не только уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явле­ния. Одним из важных выводов этой тео­рии явилось существование магнитного поля токов смещения (см. § 138), что по­зволило Максвеллу предсказать существо­вание электромагнитных волн - перемен­ного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3 10 8 м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвел­ла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857-1894), доказавшим, что законы их возбуждения и распространения полно­стью описываются уравнениями Максвел­ла. Таким образом, теория Максвелла была экспериментально подтверждена.

К электромагнитному полю применим только принцип относительности Эйнштей­на, так как факт распространения электро­магнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.

Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инер­циальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инва­риантны относительно преобразований Ло­ренца: их вид не меняется при переходе

от одной инерциальной системы отсчета к другой, хотя величины Е, В, D , Н в них преобразуются по определенным прави­лам.

Из принципа относительности вытека­ет, что отдельное рассмотрение электри­ческого и магнитного полей имеет относи­тельный смысл. Так, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь непод­вижными относительно одной инерциаль­ной системы отсчета, движутся относи­тельно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвиж­ный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке про­странства постоянное магнитное поле, дви­жется относительно других инерциальных систем, и создаваемое им переменное маг­нитное поле возбуждает вихревое электри­ческое поле. Таким образом, теория Максвелла, ее экспериментальное подтверждение, а так­же принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базиру­ющейся на представлении об электромаг­нитном поле.