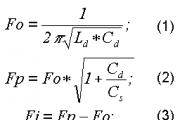Новости звезд
Напряженность электрического поля бесконечной заряженной плоскости. Поле равномерно заряженной плоскости. Поле равномерно заряженной бесконечной плоскости
Решим задачу, которая нам неоднократно понадобится в дальнейшем. Пусть электрическое поле создается зарядами, которые равномерно распределены по бесконечной плоскости.
Конечно, в реальности бесконечно больших поверхностей не существует. В данном случае, мы подразумеваем, что точка A
, в которой рассчитывается напряженность поля, находится на расстоянии h
от плоскости, которое значительно меньше расстояний до краев заряженного участка (рис. 245).
Рисунок 17 - Расчет электрического потока через несферическую поверхность. Это возможно, потому что электрический поток на поверхности не зависит от формы поверхности. Таким образом, вычисление электрического поля становится намного проще. Интересная аналогия для улучшения понимания закона Гаусса заключается в использовании световых лучей, проходящих через лампу. Пришло время выяснить, как вычислить электрическое поле по закону Гаусса для некоторых конфигураций нагрузки. Пример 1 Электрический заряд равномерно распределен вдоль бесконечного прямолинейного провода.
Рис. 245
В этом случае влияние зарядов, расположенных достаточно далеко от рассматриваемой точки становится пренебрежимо малым. Проводить расчеты для бесконечно больших плоскостей оказывается проще, чем для конечных участков.
В качестве характеристики распределения зарядов введем величину σ
− поверхностную плотность заряда. Выберем на плоскости произвольную точку с координатами (x, y
), окружим ее малой площадкой площадью ΔS
. Пусть заряд этой выделенной площадки равен ΔQ
, тогда средняя поверхностная плотность заряда определяется как отношение заряда площадки к ее площади σ = ΔQ/ΔS
. При уменьшении площади выделенной площадки, получим поверхностную плотность заряда в данной точке поверхности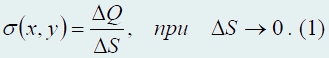
Для равномерно заряженной поверхности поверхностная плотность заряда постоянна σ(x, y) = σ = const
.
Для расчета напряженности поля воспользуемся законом Ш. Кулона и принципом суперпозиции.
Разобьем заряженную плоскость на малые участки. Такое разбиение можно проводить различными способами. Расчеты упрощаются, если мысленно разбить плоскость на тонкие кольца, а затем каждое кольцо разделить на малые участки (рис. 246).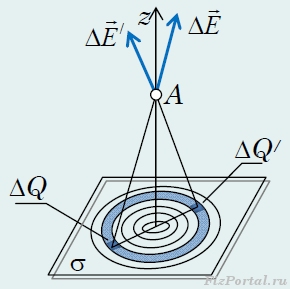
рис. 246
Каждый малый участок плоскости можно рассматривать как точечный заряд величиной ΔQ = σΔS
, который создает поле, вектор напряженности которого ΔE
направлен вдоль прямой, соединяющий заряд с точкой наблюдения A
(рис. 247).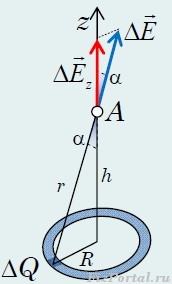
рис. 247
Полная напряженность электрического поля будет равна векторной сумме напряженностей полей, создаваемых отдельными участками плоскости. Ясно, что результирующий вектор напряженности будет направлен перпендикулярно плоскости (обозначим это направление осью z
). Действительно, для каждого заряда ΔQ
найдется симметрично расположенный заряд ΔQ /
, сумма векторов напряженностей полей ΔE + ΔE /
, создаваемых этими зарядами, будет направлена вдоль оси z
.
Вычислим напряженность поля, создаваемого равномерно заряженным кольцом, в точке находящейся на оси кольца на расстоянии h
от его центра.
Разобьем кольцо на малые участки, заряд каждого из них обозначим ΔQ i
. В точке наблюдения вектор напряженность поля ΔE i
, создаваемого этим зарядом, направлен вдоль линии, соединяющей заряд и точку наблюдения. Величина этого вектора может быть рассчитана по закону Ш. Кулона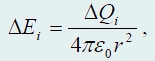
где r = √{h 2 + R 2 }
− расстояние от заряда то точки наблюдения.
Как мы показали, результирующий вектор напряженности направлен вдоль оси кольца. Поэтому для его расчета достаточно просуммировать проекции векторов ΔE
на эту ось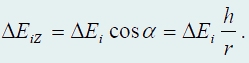
Просуммируем проекции векторов напряженностей полей, создаваемых всеми зарядами, на которые мы разбили кольцо
Так как все заряды находятся на равных расстояниях r от точки наблюдения, а векторы ΔEi образуют равные углы α с осью z, вычисление этой суммы сводится суммированию зарядов (постоянные множители можно вынести за знак суммы):
Заметим, что в центре кольца напряженность поля равна нулю, затем с ростом h
напряженность поля возрастает до некоторого максимального значения, после чего начинает монотонно убывать. Причем на больших расстояниях при h >> R
в формуле (2) можно пренебречь R
в знаменателе, при этом напряженность поля определяется формулой E z ≈ Q/(4πε o h 2)
, которая соответствует напряженности поля точечного заряда. Данный результат понятен, на расстояниях значительно превышающих радиус кольца, кольцо можно рассматривать как точечный заряд. График функции (2) показан на рисунке 248.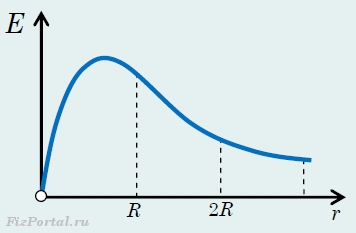
рис. 248
Далее для вычисления напряженности поля, созданного всей плоскостью, необходимо просуммировать выражения (2) по всем кольцам, на которые была разбита плоскость. Такое суммирование, в принципе, можно провести, но этот расчет требует привлечения операции интегрирования, поэтому заниматься этим не будем. Тем более, что результат можно получит гораздо быстрее, использую теорему Гаусса.
Для использования этой теоремы для определения напряженности поля, необходимо рассмотреть симметрию поля, которая, очевидно связана с симметрией зарядов. Распределение зарядов не изменится, если плоскость сместить на любой вектор a
, лежащий в самой плоскости. Поэтому при таком смещении не изменится и напряженность поля (рис. 249).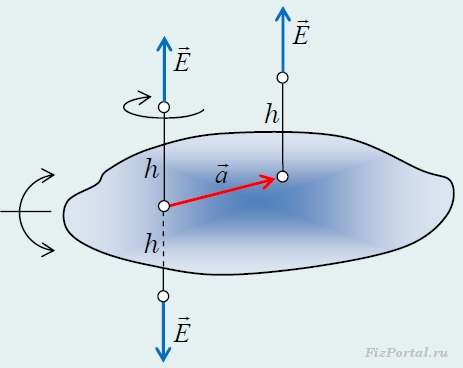
рис. 249
Следовательно, напряженность поля может зависеть только от расстояния до плоскости h
. Любая прямая, перпендикулярная плоскости является осью симметрии, то есть при повороте плоскости на любой угол относительно любой оси, перпендикулярной плоскости, распределение зарядов не изменяется − следовательно, и вектор напряженности при таком повороте не изменится, поэтому этот вектор должен быть перпендикулярен плоскости. Наконец, заряженная плоскость является плоскостью симметрии для поля. Поэтому в симметричных точках векторы напряженности также симметричны. Выявленные свойства симметрии электрического поля позволяют выбрать поверхность, для которой можно выразить поток вектора напряженности в простой форме. Итак, в качестве такой поверхности выберем поверхность прямого цилиндра, образующие которого перпендикулярны плоскости, а основания площадью S
параллельны ей и находятся на равных расстояниях от плоскости.
Прежде всего, заметим, что поток вектора напряженности через боковую поверхность цилиндра равен нулю, так как во всех точках боковой поверхности векторы напряженности E
и нормали n
взаимно перпендикулярны (поэтому cosα = 0
) (рис. 250).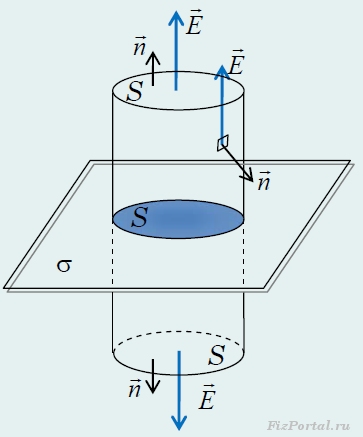
рис. 250
Поток через верхнее основание цилиндра может быть записан в виде Ф = ES
, так модуль напряженности поля на основании цилиндра постоянен, а по направлению совпадает с вектором нормали. Такое же значение имеет поток через нижнее основание. Таким образом, суммарный поток вектора напряженности электрического поля через поверхность цилиндра равен Ф E = 2ES
. По теореме Гаусса этот поток равен заряду внутри поверхности Q = σS
, деленному на электрическую постоянную Ф E = 2ES = σS/ε o
. Их этого равенства выражаем модуль вектора напряженности электрического поля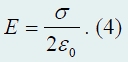
Как видите, с использованием теоремы Гаусса нам удалось решить поставленную задачу «в одно действие». Главная составляющая успеха − анализ симметрии поля, позволивший разумно выбрать поверхность, для использования теоремы Гаусса. Также обратите внимание, что напряженность данного поля одинакова во всех точках, следовательно, это поля является однородным. Подчеркнем, независимость напряженности поля от расстояния до плоскости h
никак не следует из симметрии поля, это результат нашего расчета.
Нагрузка на единицу длины определяется как положительная λ. Вычислите электрическое поле этой конфигурации. Разрешение. Мы видим, что это представление приближается к распределению нагрузки конечного прямолинейного провода, если расстояние между точкой поля и проводом намного меньше его длины. Чтобы начать расчет, сначала нужно определить, какой тип симметрии допускает распределение нагрузки. В этом случае система имеет цилиндрическую симметрию. Когда заряды положительны, электрическое поле указывает на поверхность.
Мы можем составить схему ситуации, чтобы визуализировать ее лучше. Рисунок 18 - Коаксиальная цилиндрическая гауссовская поверхность используется для определения электрического поля, создаваемого снаружи бесконечно длинного заряженного провода. Заметим, что линии электрического поля равномерно заряженного бесконечного прямолинейного провода являются радиальными и содержатся в плоскостях, перпендикулярных проволоке. Таким образом, модуль электрического поля может зависеть только от радиального расстояния между точкой и проводом.
Использование теоремы Гаусса для расчета полей эффективно в тех случаях, когда поле обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической). Симметрия и конфигурация поля должны быть такими, чтобы, во-первых, заряженное тело можно было бы окружить достаточно простой замкнутой поверхностью и, во-вторых, вычисление потока вектора напряженности свести к простому умножению Е (или E n) на площадь поверхностиSили часть ее. Если этого сделать нельзя, то задачу необходимо решать другими методами.
Обратите внимание, что на нашей цилиндрической поверхности имеются три области: цилиндр, который окружает провод и обе стороны. Поскольку мы знаем, что провод бесконечен, все линии электрического поля перпендикулярны проволоке, поэтому на боковых поверхностях нет потока электрического поля. Остается определить электрическое поле на цилиндрической поверхности вокруг провода. Соблюдайте закон Гаусса, чтобы запомнить, какую информацию вам нужно определить.
Поскольку он имеет постоянное значение, мы можем извлечь его из процедуры интеграции. Цилиндра можно получить, умножив длину окружности цилиндра на длину цилиндра. Таким образом, выражение суммируется следующим образом. Полученный внутренний заряд может быть получен путем умножения плотности заряда на всю длину поверхности.
Поле равномерно заряженной бесконечной плоскости
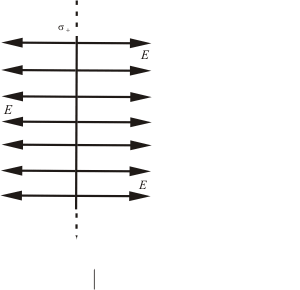
Будем считать заряд положительным. Плоскость заряжена с постоянной поверхностной плотностью . Из симметрии вытекает, что напряженность в любой точке поля имеет направление, перпендикулярное к плоскости (рис. 2.10). Очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению.
То есть, электрическое поле в этом случае будет. Что является тем же результатом, полученным при вычислении с использованием кулоновской формы. Но теперь наша работа была намного меньше. 23. Хотя закон Гаусса определяется как интегральная функция, во многих случаях нет необходимости решать интеграл, потому что достаточно найти подходящую поверхность и выражение для вычисления площади этой поверхности. Представьте, что вы выполняете тот же расчет, используя закон Кулона!
Пример 2. Разрешение: Представленная ситуация имеет сферическую симметрию. Тогда выбранная гауссова поверхность будет сферической и концентрической по отношению к распределению заряда. В этом случае электрическое поле будет радиально от поверхности и нормали к площади поверхности. Соблюдайте контур ситуации. Таким образом, закон Гаусса можно записать в виде. Его можно определить, используя определение объемной плотности следующего выражения. Объем гауссовой поверхности определяется следующим образом.
Выделим на заряженной плоскости площадку
.
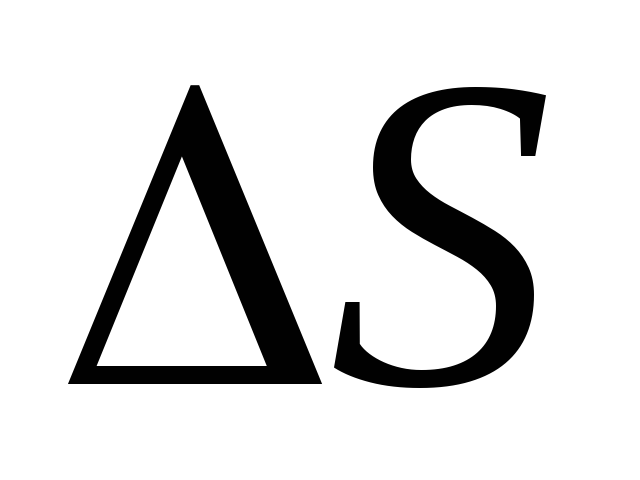Окружим эту площадку замкнутой
поверхностью. В качестве замкнутой
поверхности представим цилиндрическую
поверхность с образующими, перпендикулярными
к плоскости и основаниями величины
,
расположенными относительно плоскости
симметрично. Применим к этой поверхности
теорему Гаусса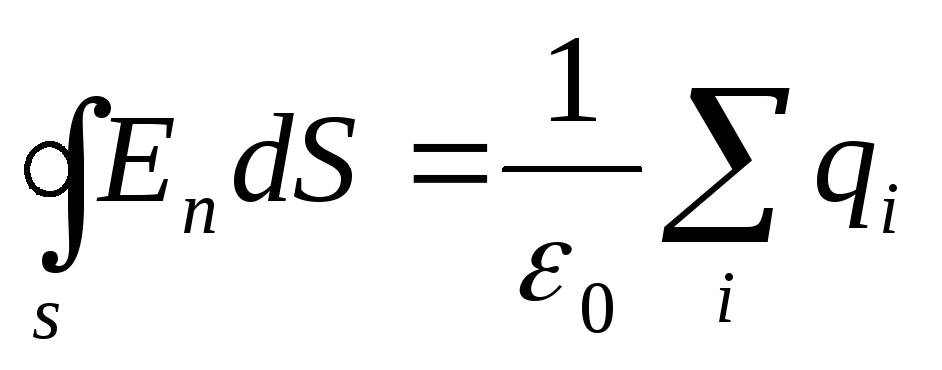
.
Поток через боковую часть поверхности
будет отсутствовать, так как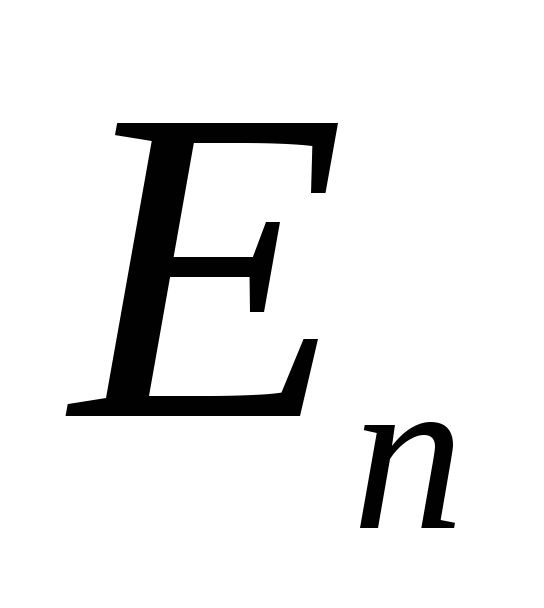
в каждой ее точке равна нулю. Для оснований
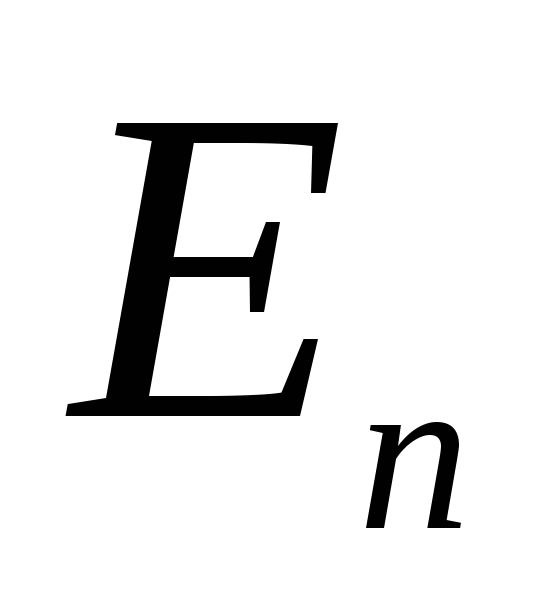совпадает с
.
Следовательно, суммарный поток через
поверхность будет равен
.
Внутри поверхности заключен заряд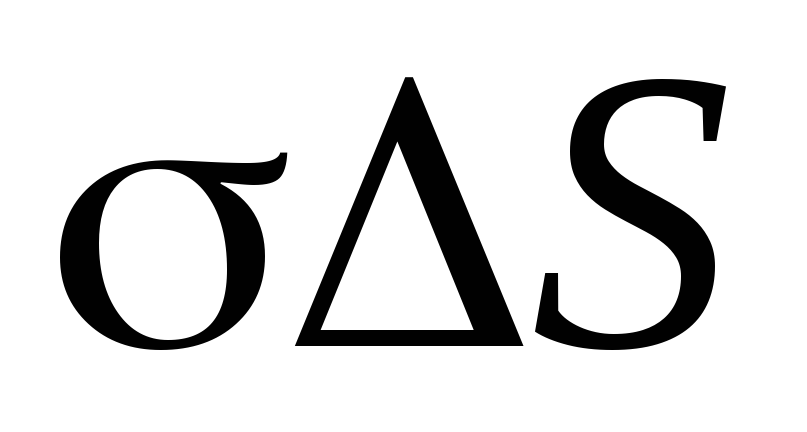
.
Согласно теореме Гаусса, должно
выполняться условие:
,
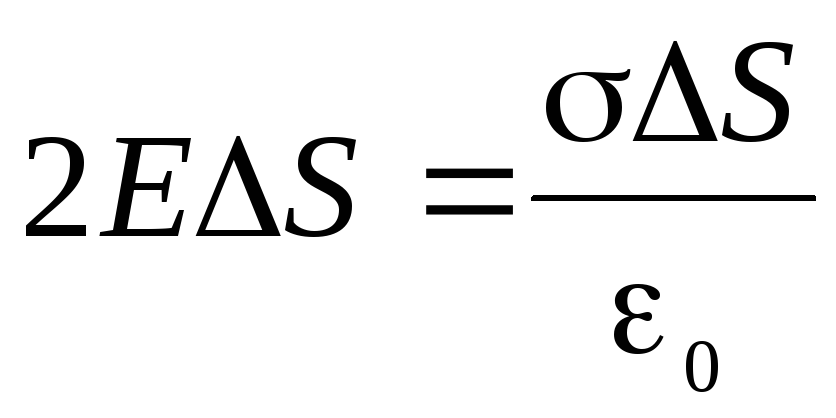откуда
Заменив этот результат выражением закона Гаусса в начале резолюции, мы получим. Таким образом, мы получаем выражение, определяющее электрическое поле на гауссовой поверхности внутри сферической изоляции. Просто замените значения в полученном выражении. Выражение для определения электрического поля было бы следующим. Если бы мы имели дело с проводящей поверхностью, электрическое поле в любой точке внутри него было бы нулевым, так как весь заряд распределялся бы на концах проводника из-за электрического отталкивания между зарядами.
Уже для точки вне проводящей поверхности выражение будет таким же, как и полученное ранее. В этом примере мы завершили наш первый урок, в котором вы изучили важные концепции, лежащие в основе всех знаний о электрических явлениях. Связанные с электрическими зарядами являются процессами электрификации, ответственными за несколько явлений, с которыми мы сталкиваемся каждый день: электризация трения и электризация индукции. Вы также изучили, что электрические заряды создают нарушение в пространстве, называемое электрическим полем, которое может быть представлено силовыми линиями.
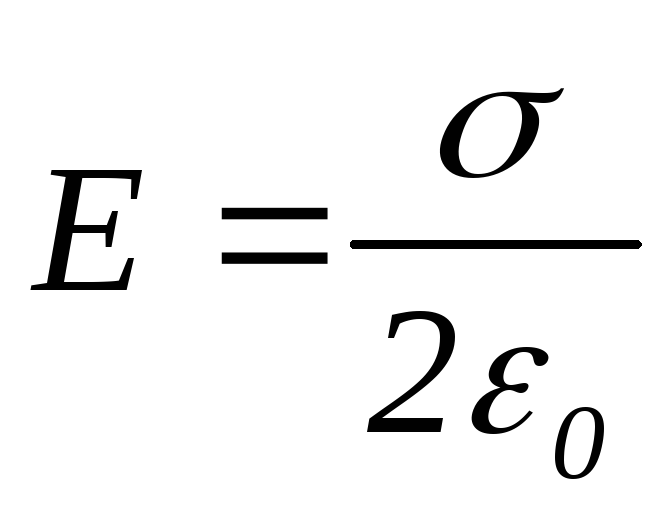
. (3)
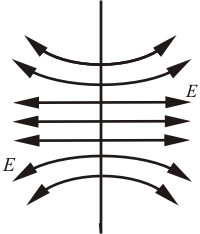
Полученный результат не зависит от длины цилиндра, т.е. на любых расстояниях от плоскости напряженность поля одинакова по величине. Картина линий напряженности выглядит, как показано на рис. 2.11. Для отрицательно заряженной плоскости направления векторов изменятся на обратные. Если плоскость конечных размеров, то полученный результат будет справедлив лишь для точек, расстояние которых от края пластины значительно превышает расстояние от самой пластинки (рис. 2.12).
Это поле создает силу для других электрических зарядов, которые могут быть определены Законом Кулона или Законом Гаусса. Например, если бы мы хотели знать электрическое поле вблизи земной поверхности, у нас было бы достаточно информации о распределении заряда на поверхности, и мы могли бы легко определить электрическое поле в нужной области. В следующем классе вы изучите электрический потенциал. Основываясь на этих знаниях, вы будете готовы применить свои исследования в решении проблем, связанных с электрическими конденсаторами, электрическими токами и цепями, которые будут представлены в более поздних классах.
|
|
|
Поле, образованное двумя разноименными заряженными плоскостями (бесконечно большими)
Поле двух параллельных бесконечно
больших плоскостей, заряженных разноименно
с одинаковой по величине постоянной
поверхностной плотностью
можно рассматривать как суперпозицию
полей, создаваемых каждой из плоскостей
в отдельности. В области между плоскостями
(рис.2.13) складываемые поля имеют одинаковое
направление, так что результирующая
напряженность равна
Вы видели, что заряды взаимодействуют друг с другом через электрическое поле и сигнал заряда, создавая электрическую силу. Мы знаем, что работа электронных устройств, например лампочек, зависит от наличия электроэнергии. Но как можно связать понятие энергии с электрическими зарядами? В этом уроке вы увидите одно из понятий, которые помогут вам понять эту проблему: электрический потенциал. Помимо обеспечения энергии, которая делает работу электронного оборудования, электрический потенциал связан с другим интересным явлением: электрическими разрядами, возникающими во время штормов.
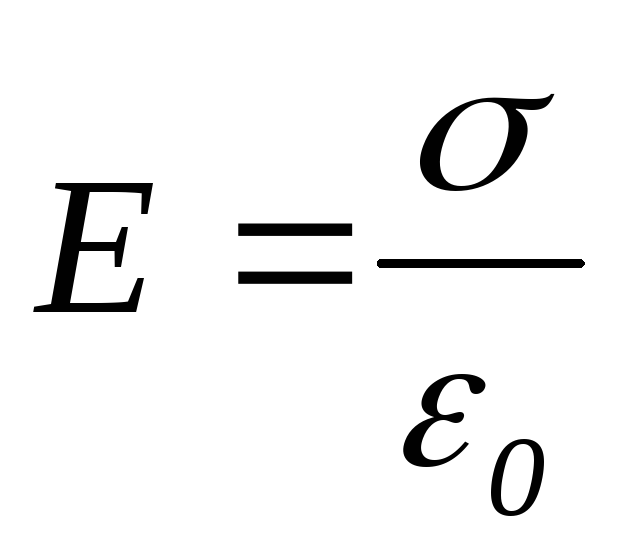
(4)
Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулюE =0 . Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими свойствами, называетсяоднородным . Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых.
Вы знаете, как происходят эти процессы? Продолжайте читать этот и предстоящие уроки, и вы получите ответы! В механике потенциальная энергия является мерой энергии, связанной с состоянием, в котором тело с массой находится в поле силы тяжести. Следующий рисунок. Объект, движущийся в однородном гравитационном поле. Рисунок 13 - Объект, движущийся в однородном гравитационном поле.
Таким образом, работа, выполняемая полем, может быть записана как: 28. Это связано с тем, что по мере падения объекта работа происходит в направлении поля, поэтому она положительна, и в этом случае потенциальная энергия тела уменьшается. Если объект был взят вверх, работа, выполняемая гравитационным полем, была бы отрицательной, поскольку она противоречит направлению движения.
Полученный результат приблизительно справедлив и в случае плоскостей конечных размеров, если расстояние между плоскостями значительно меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности напряженности наблюдаются только вблизи краев пластин (рис. 2.14).
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ .
Однако изменение потенциальной энергии было бы положительным, т.е. тело увеличивало бы свою потенциальную энергию. Механика может быть решена легче, чем при использовании законов Ньютона. Вы увидите, что та же концепция может быть применена к электрическим явлениям.
Мы можем понять потенциал, поскольку количество энергии, которое система может обеспечить для электрического заряда. Обратите внимание на следующий рисунок. Рисунок 14 - Положительный заряд перемещается внутри электрического поля в том же направлении поля и в противоположном направлении.
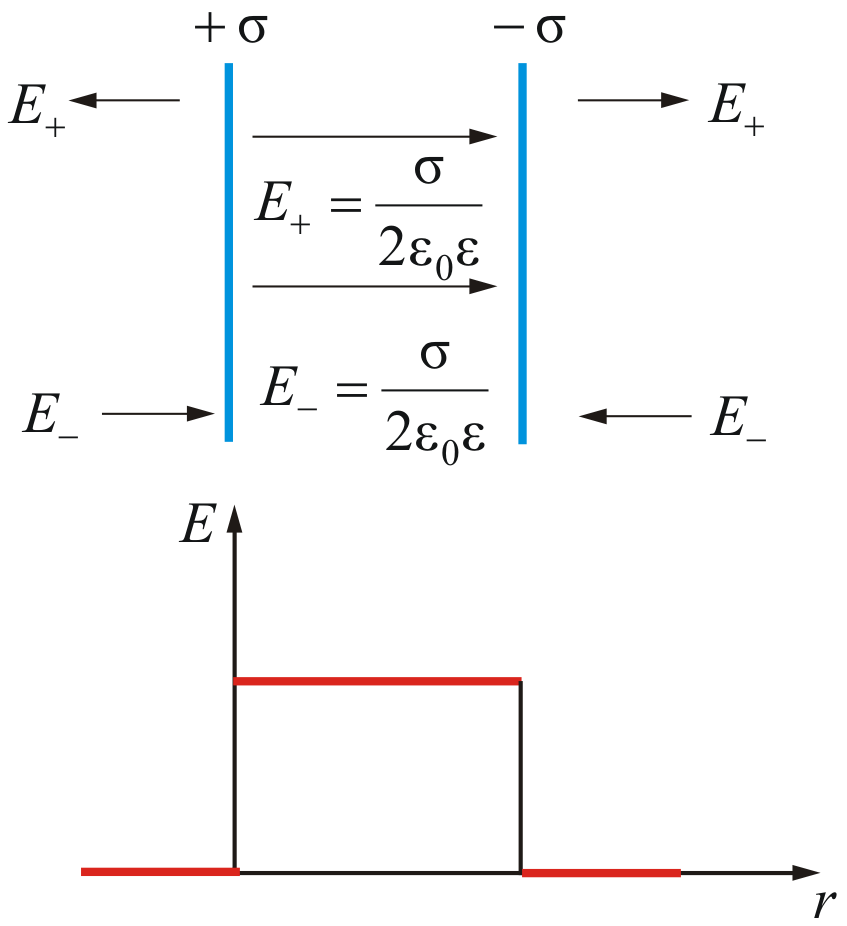
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей
Вне плоскостей
напряженность поля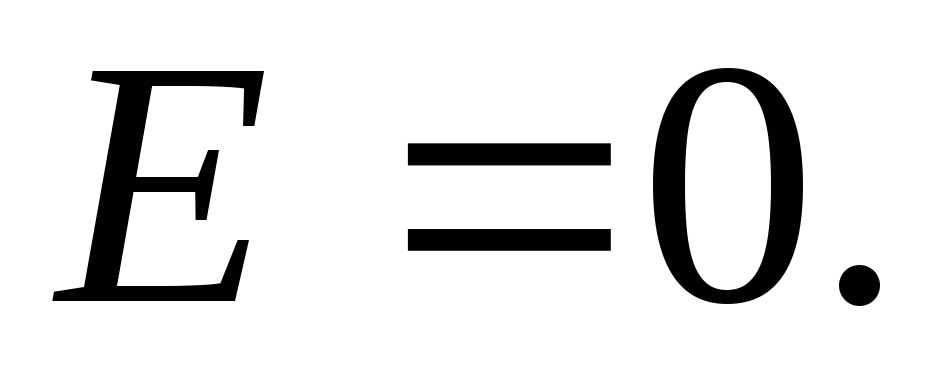
.
В котором он представляет собой очень малую составляющую смещения нагрузки по траектории. Таким образом, мы можем написать следующее. С учетом нашего примера происходит то же самое. Если бы это было отрицательно, потенциальная энергия увеличивалась бы, когда она двигалась в направлении поля и уменьшалась бы, если бы она двигалась в противоположном направлении. Такое поведение напоминает силу гравитационной потенциальной энергии, в которой тело, поднятое вверх, увеличивает свою потенциальную энергию - потому что оно движется в обратном направлении к полю - и уменьшает свою гравитационную потенциальную энергию, когда она опускается, перемещаясь в том же направлении, что и поле.
Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке.
Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
,
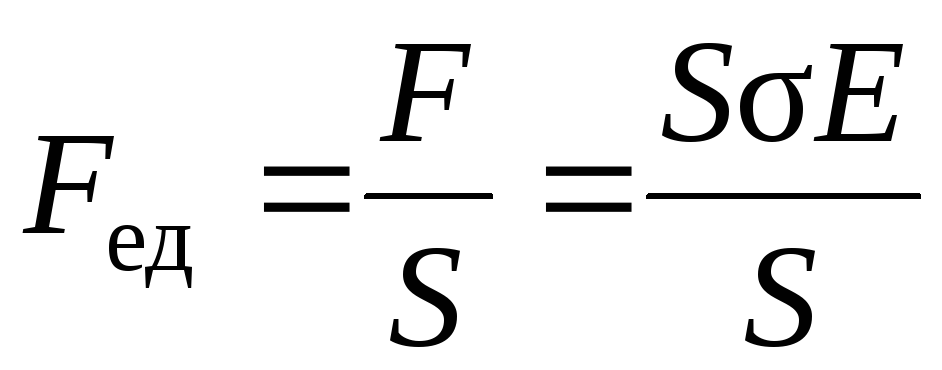т.е.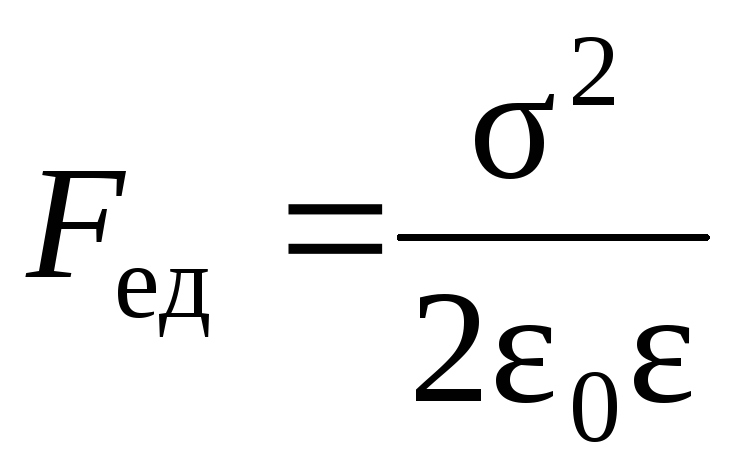
.
Изменение энергии электрического потенциала может быть записано как функция интеграла, представленного в выражении. Заметим, что потенциальная энергия является характеристикой системы зарядового поля, обусловленной взаимодействием поля с заряженной частицей внутри поля. Из этой идеи мы определяем другое понятие: электрический потенциал, зависящий только от характеристик поля, независимо от существования заряженной частицы в поле.
Вопреки распространенному мнению, напряжение не то, что движется через систему, а скорее различие в энергии за заряд между двумя точками. Например, общая щелочная батарея имеет возможность обеспечивать 1, 5 В энергии для каждой зарядки, которая будет составлять электрический ток.
Механические силы, действующие между заряженными телами, называют пондермоторными.
Тогда сила притяжения между пластинами конденсатора:
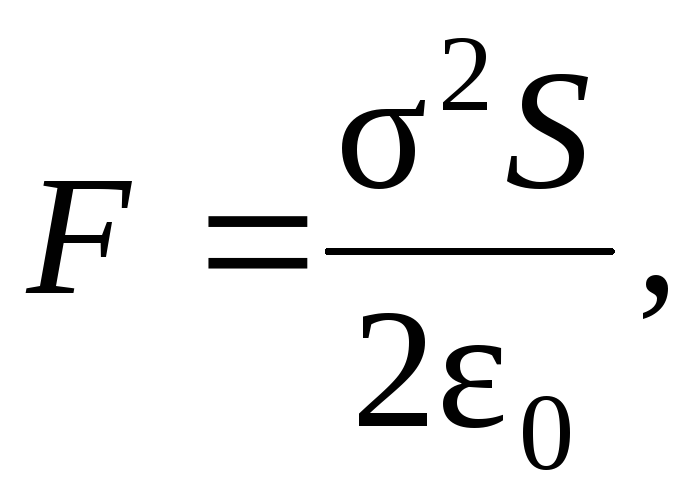
где S
– площадь обкладок
конденсатора. Т.к.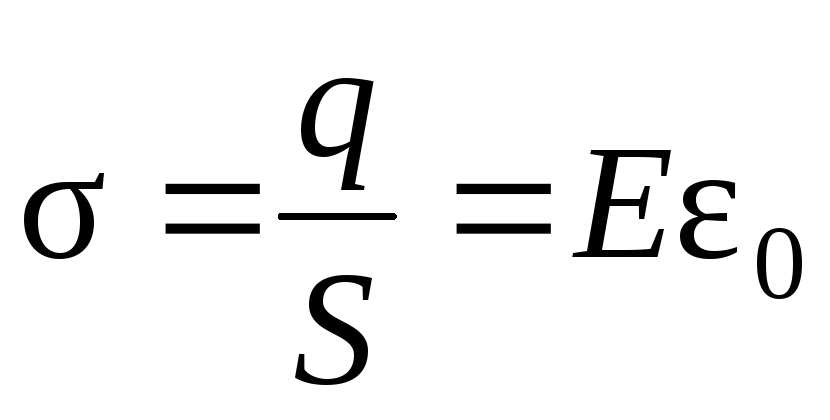
,
то
Теперь, когда вы знакомы с концепциями электрического потенциала, электрического потенциала и разности электрических потенциалов, пришло время изучить потенциал некоторых систем нагрузки. Источник: Адаптировано от Сирса и Джуветта. Зная, что электрическое поле в любой точке пространства для точечного заряда равно. Мы можем переписать его так.
Заменяя этот результат в предыдущем выражении и переставляя его, получим: и, решая интеграл, получим. Удобно выбрать точку, в которой электрический потенциал равен нулю, полученному на бесконечности. Таким образом, выражение выше: Это выражение называется кулоновским потенциалом. Максимальная нагрузка. Слишком далеко от нагрузки потенциал минимален, т.е. взаимодействие между зарядами отсутствует.
.
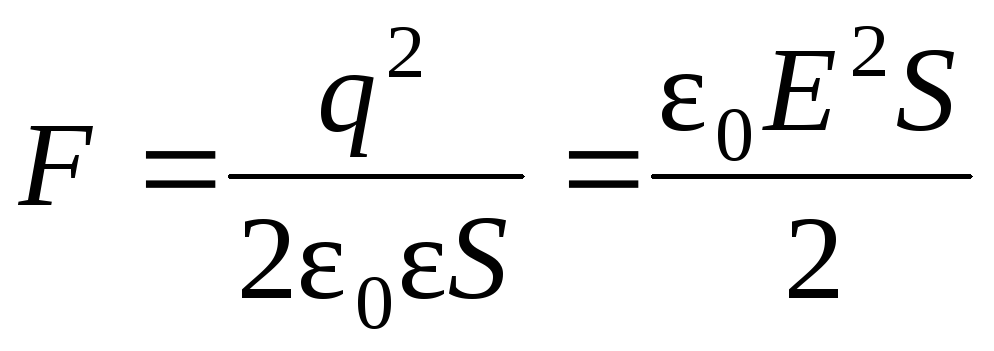Это формула для расчета пондермоторной силы.
